The Heat Equation
The one dimensional homogeneous heat equation is given by \[u_t-c^2u_{xx}=0.\]
The maximum principle
The maximum principle states that if the function \(u(x,t)\) satisfies the homogeneous heat equation \(u_{t}-c^2u_{xx}=0\) for \(x\in[0,l], t\in[0,T]\), then the function \(u(x,t)\) attains its maximum value somewhere on the parabolic boundary \[\Pi = \left([0,l]\times\{0\}\right)\cup\left(\{0\}\times[0,T]\right)\cup\left(\{l\}\times[0,T]\right).\]
Solution on a finite length rod
Much like the wave equation problem on a finite-length string, this is a Sturm-Liouville problem. Accordingly, it can be solved in much the same way by seeking a separable solution in the form \[u(x,t)=X(x)T(t),\]and substiuting into the PDE to obtain an ODE, both sides of which must be equal to a constant since one side depends only on \(t\) and the other only on \(x\). Of course, because the heat equation only has one derivative with respect to time, the key difference that you'll find between this problem and the similar wave equation problem is that the ODE for \(T(t)\) will be of first order (rather than second order).
Below is an animation of a solution to such a problem, with endpoints of the rod held at constant temperature 0\(^\circ\)C and sinusoidal initial temperature as stated in the title of the plot. Note how the heat equation 'smooths everything out'; this is the classic behaviour of solutions to parabolic PDEs.
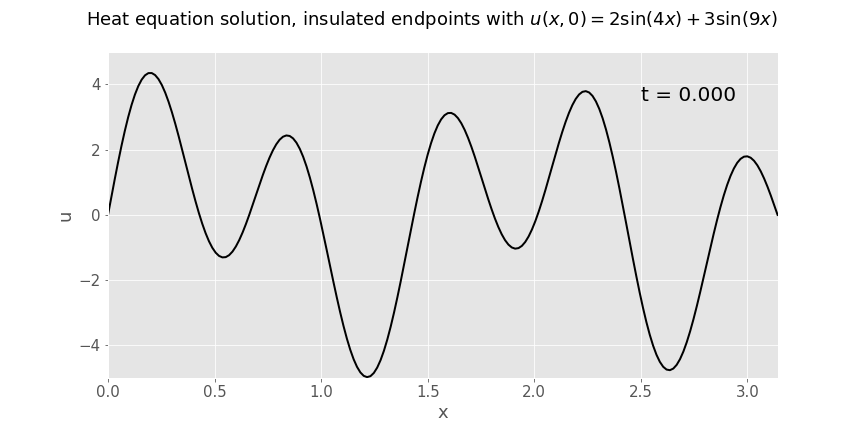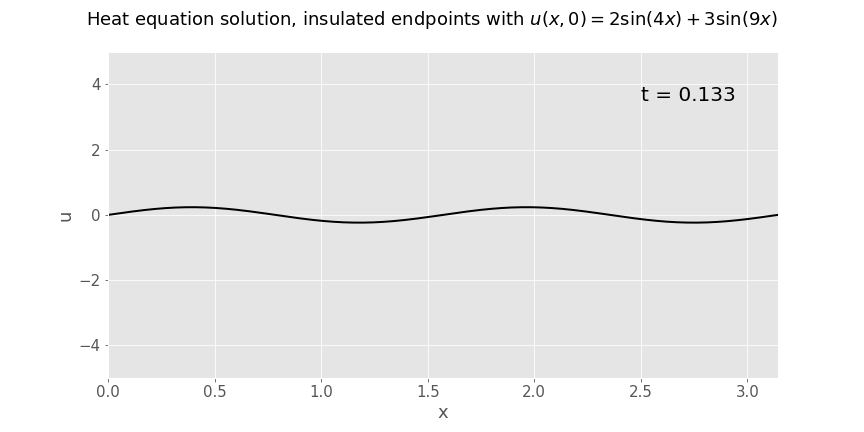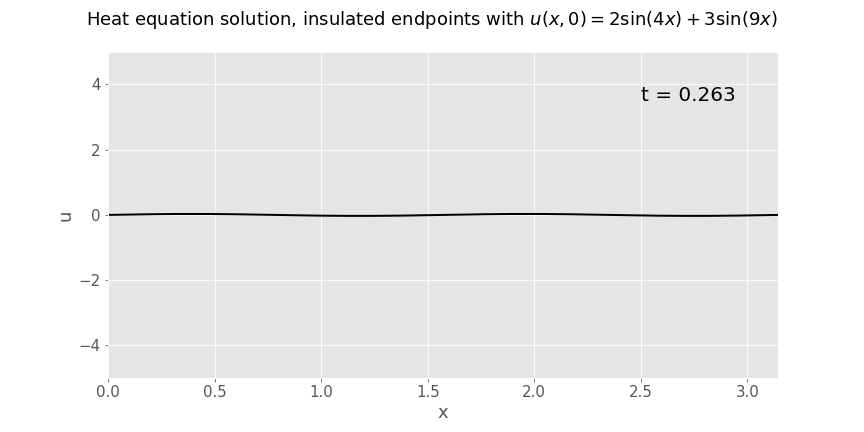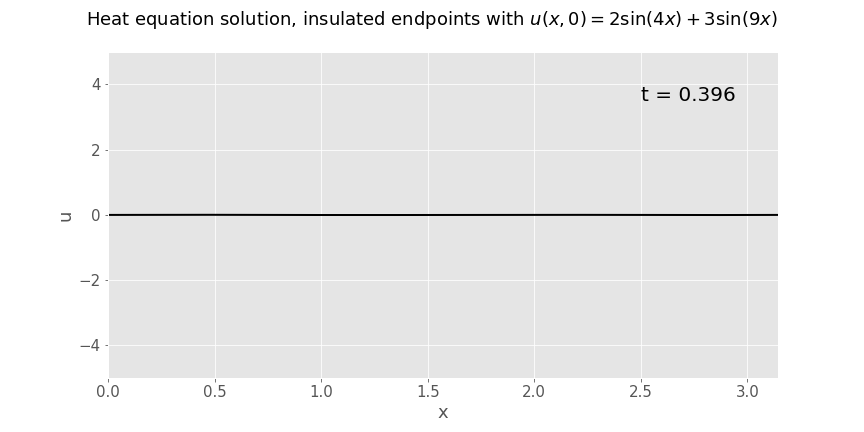
Solution on an infinite length rod
This problem is trickier! We'll use Fourier transforms to solve it; see the video on the Fourier Transforms page and your notes from lectures.
The Heat Equation
The one dimensional homogeneous heat equation is given by \[u_t-c^2u_{xx}=0.\]
The maximum principle
The maximum principle states that if the function \(u(x,t)\) satisfies the homogeneous heat equation \(u_{t}-c^2u_{xx}=0\) for \(x\in[0,l], t\in[0,T]\), then the function \(u(x,t)\) attains its maximum value somewhere on the parabolic boundary \[\Pi = \left([0,l]\times\{0\}\right)\cup\left(\{0\}\times[0,T]\right)\cup\left(\{l\}\times[0,T]\right).\]
Solution on a finite length rod
Much like the wave equation problem on a finite-length string, this is a Sturm-Liouville problem. Accordingly, it can be solved in much the same way by seeking a separable solution in the form \[u(x,t)=X(x)T(t),\]and substiuting into the PDE to obtain an ODE, both sides of which must be equal to a constant since one side depends only on \(t\) and the other only on \(x\). Of course, because the heat equation only has one derivative with respect to time, the key difference that you'll find between this problem and the similar wave equation problem is that the ODE for \(T(t)\) will be of first order (rather than second order).
Below is an animation of a solution to such a problem, with endpoints of the rod held at constant temperature 0\(^\circ\)C and sinusoidal initial temperature as stated in the title of the plot. Note how the heat equation 'smooths everything out'; this is the classic behaviour of solutions to parabolic PDEs.

Solution on an infinite length rod
This problem is trickier! We'll use Fourier transforms to solve it; see the video on the Fourier Transforms page and your notes from lectures.