d'Alembert's equation
d'Alembert's equation gives the solution of the homogeneous wave equation \(u_{xx}-c^2u_{tt}=0\) subject to initial conditions that define the original displacement profile (that is \(u(x,0)=f(x)\)) and an initial velocity profile \(\text{(i.e. }u_t(x,0)=g(x)\text{).}\) The solution is then given by \[u(x,t)=\frac{1}{2}(f(x+ct)+f(x-ct))\goodbreak{}+\frac{1}{2c}\int\limits_{x-ct}^{x+ct}g(\lambda)\mathrm{d}\lambda.\] Such a problem with initial conditions is known as a Cauchy problem.
Derivation of d'Alembert's equation
Solution on a finite-length string
The wave equation on a finite-length string with suitable initial and boundary conditions (e.g. fixed endpoints) is an example of a Sturm-Liouville problem. It can be solved by seeking a separable solution in the form \[u(x,t)=X(x)T(t).\] Substituting this assumed form into the PDE and rearranging, one can reduce the problem to two second order ODEs, one for \(X(x)\) and another for \(T(t)\). This arises since one side of the resulting ODE is a function of \(t\) only, while the other is a function only of \(x\); since these are independent variables it must be true that both sides are equal to a constant. Upon solving the problem for \(X(x)\) we'll usually discover that non-trivial solutions only exist for certain values of the aforementioned constant. We call such values eigenvalues.
The superposition principle allows us to write the solution in the form of an infinite series. We then use Fourier series in order to determine coefficients in the general solution that enable initial conditions to be satisfied.
See your notes from the lectures for the detail.
Duhamel's equation - inhomogeneous wave equation
The inhomogeneous one-dimensional wave equation is given by \[u_{tt}-c^2u_{xx}=h(x,t).\] The presence of the function \(h(x,t)\) models a source of waves.
In the lectures we've seen that the solution to the inhomogeneous wave equations with homogeneous initial conditions\[u(x,0)=0,\]\[u_t(x,0)=0,\] is given by \[u(x,t)=\frac{1}{2c}\int\limits_{0}^t\int\limits_{x-c(t-\tau)}^{x+c(t-\tau)}h(y,\tau)\mathrm{d}y\mathrm{d}\tau.\]
Derivation of Duhamel's equation
Animations of solutions to the homogeneous wave equation
The following are all animations illustrating solutions to the Cauchy problem for the 1D homogeneous wave equation \[u_{tt}-c^2u_{xx}=0,\] with initial conditions \(u(x,0)=f(x)\) and \(u_t(x,0)=g(x)\). As we've seen in lectures, solutions to this problem are given by d'Alembert's formula: \[u(x,t)=\frac{1}{2}\{f(x-ct)+f(x+ct)\}+\frac{1}{2c}\int\limits_{x-ct}^{x+ct}g(\lambda)\mathrm{d}\lambda.\]
In all cases plotted below, \(c=1\).
Straightforward plots of d'Alembert's solution
If you want to play around and make your own, click for the Python source.
Gaussian (\(e^{-x^2}\)) initial displacement, zero initial velocity
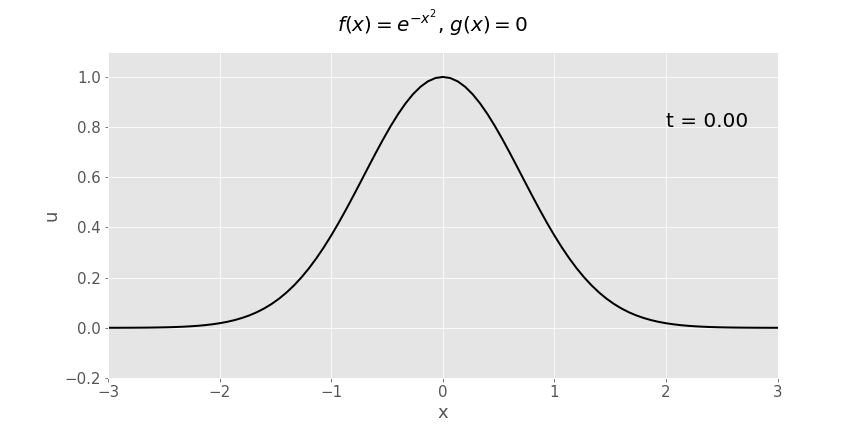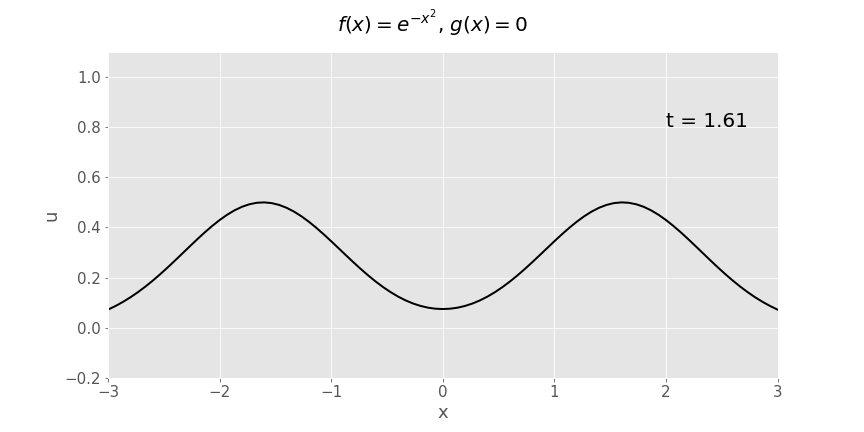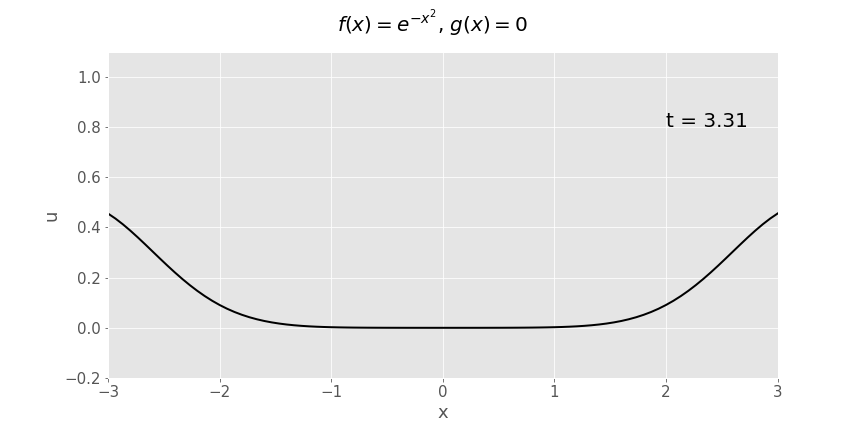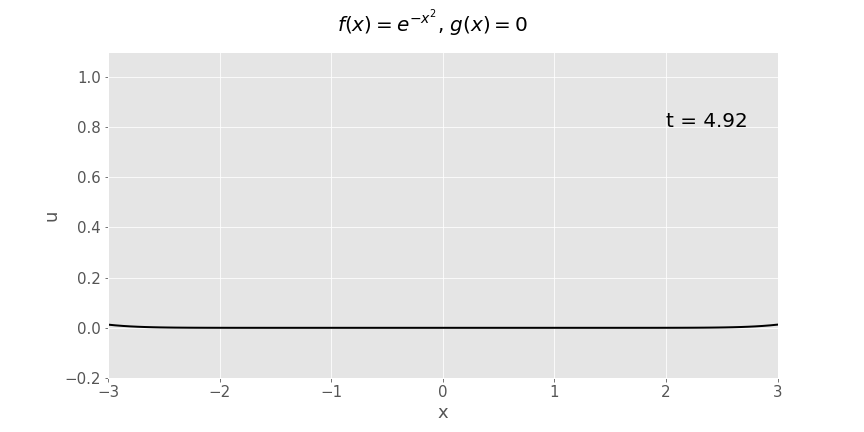
Another way of plotting exactly the same function of \(x\) and \(t\) is as a surface plot:
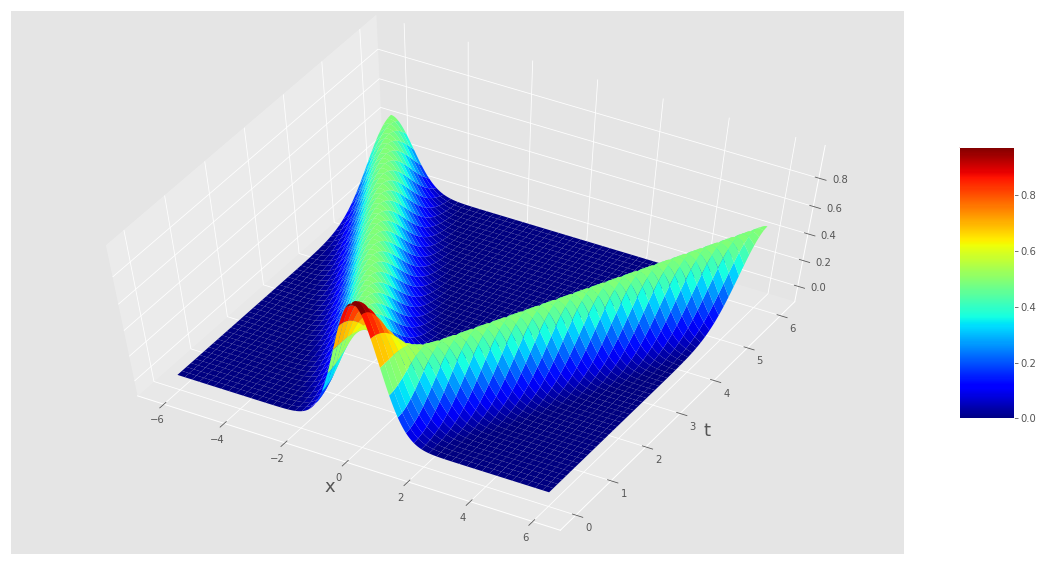
Note the similarities between this plot and the sketches we've drawn in lectures when disucssing ideas related to causality.
Gaussian (\(e^{-x^2}\)) initial displacement, sinusoidal initial velocity (\(\frac{1}{10}\sin x\))
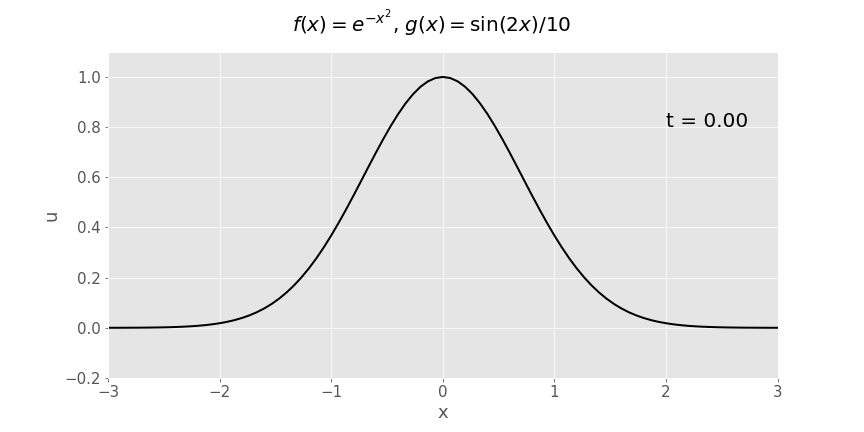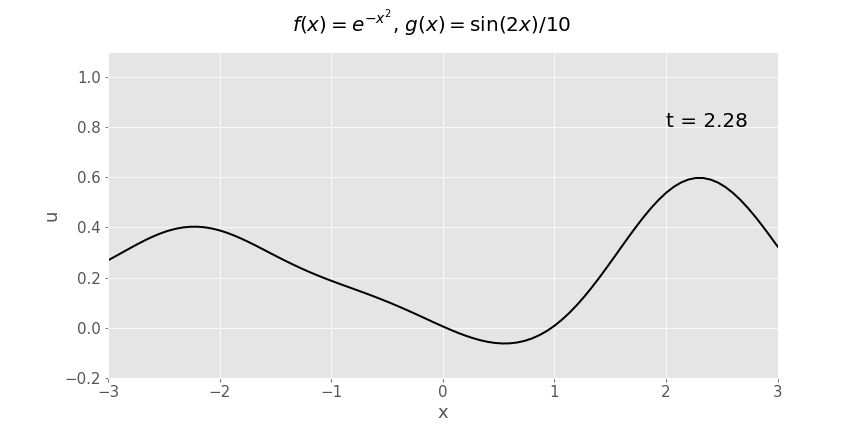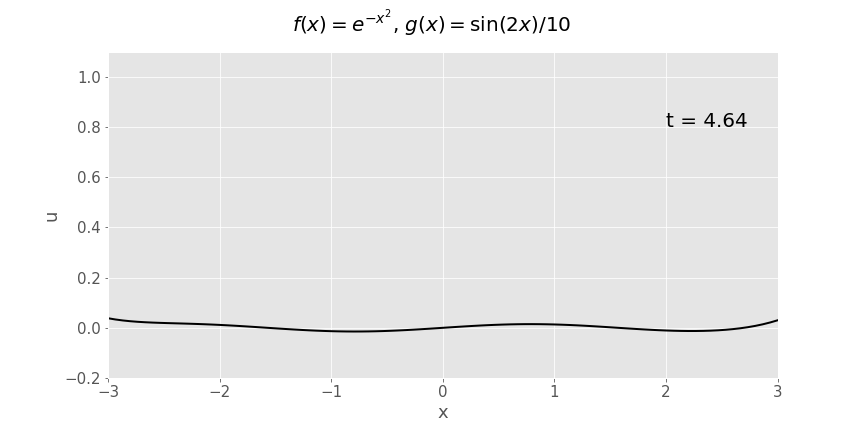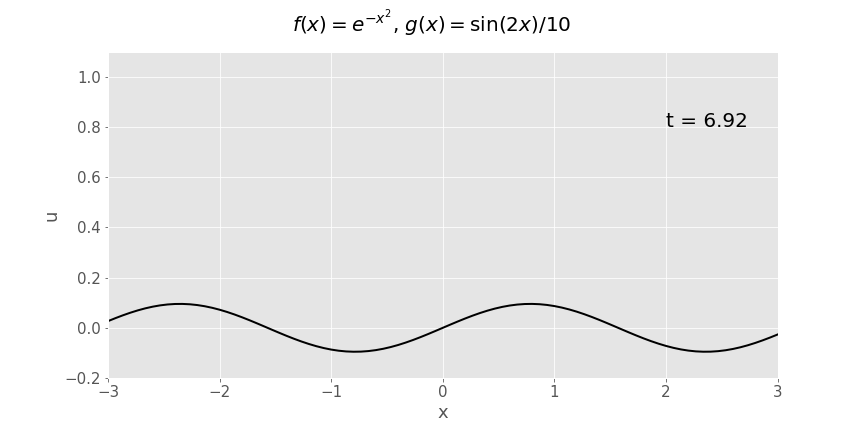
Reflection
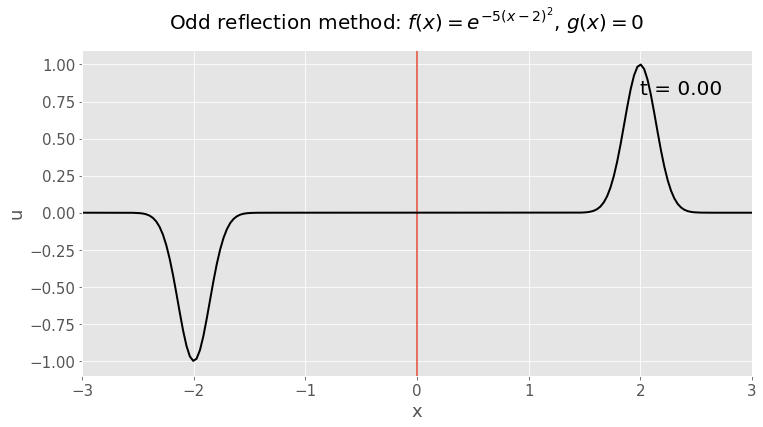
Suppose we want to solve the wave equation on a semi-infinite string occupying \(x>0\), with initial displacment \(u(x,0)=f(x)=e^{-5(x-2)^2}\) and initial velocity \(u_t(x,0)=g(x)=0\). At the end of the string (\(x=0\)), we fix the displacement to be zero, so \(u(0,t)=0\) for all \(t>0\).
We've seen in lectures that the way to tackle this problem is odd reflection, in which we extend the initial conditions by reflecting them in an odd fashion so they're defined for all \(x\in\mathbb{R}\).
This is shown in the animation below. The first image is a still of the initial condition, so you can see clearly the odd reflection.
Here's the animation if we let time run:
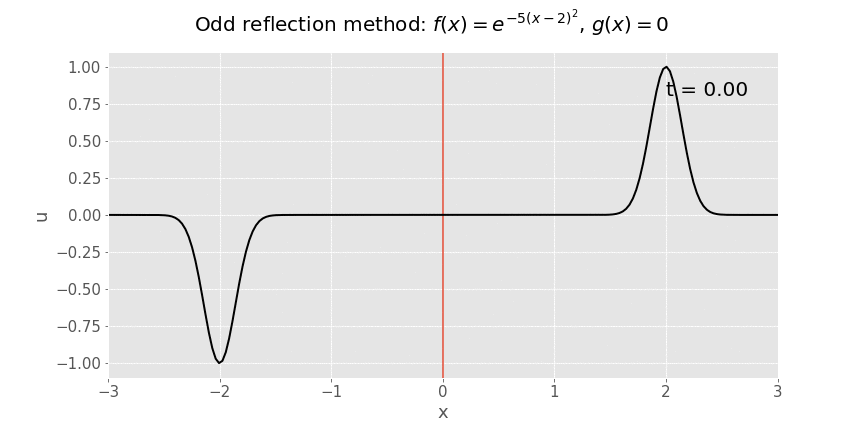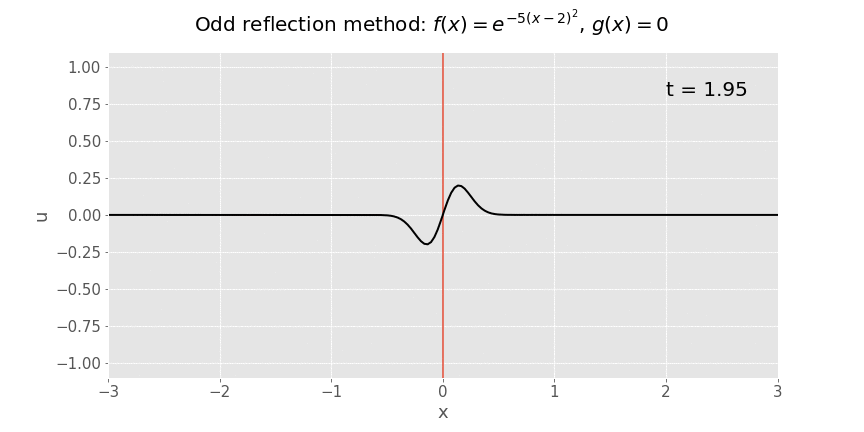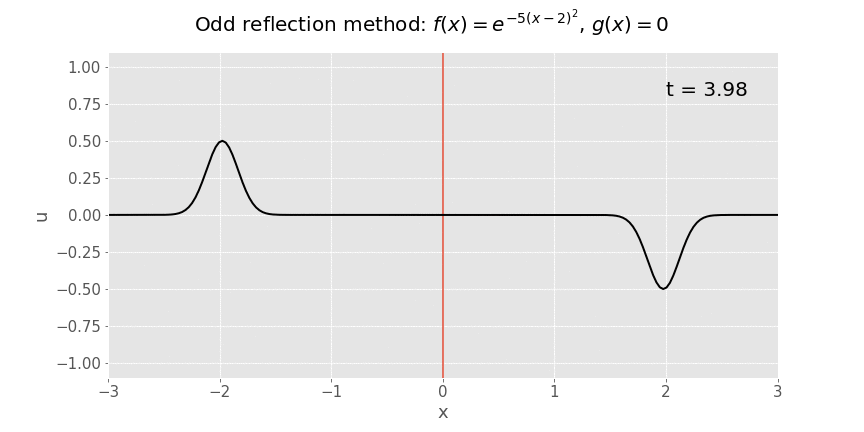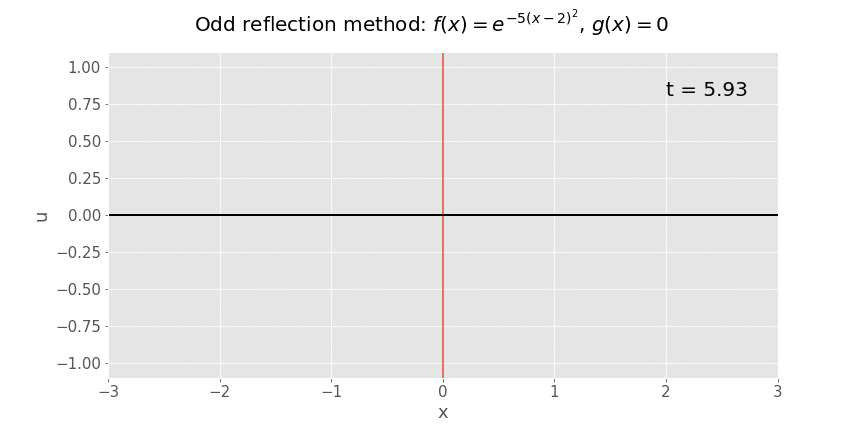
The solution to the original problem is the restriction of the solution to positive \(x\), i.e. everything to the right of the red line. Everything to the left of the red line is solely a mathematical tool which has allowed us to use d'Alembert's formula. The odd nature of the reflection ensures that the boundary condition at the string's endpoint is satisfied.
Click here for an extra example of reflection, with some explanation.
Hafaliad d'Alembert
Mae hafaliad d'Alembert yn rhoi datrysiad yr hafaliad ton homogenaidd \(u_{xx}-c^2u_{tt}=0\) yn ddibynnol ar yr amodau cychwynnol sy'n diffinio'r proffil dadleoliad (hynny yw \(u(x,0)=f(x)\)) a'r proffil cyflymder cychwynnol \(\text{(h.y. }u_t(x,0)=g(x)\text{).}\) Yna rhoir y datrysiad fel \[u(x,t)=\frac{1}{2}(f(x+ct)+f(x-ct))\goodbreak{}+\frac{1}{2c}\int\limits_{x-ct}^{x+ct}g(\lambda)\mathrm{d}\lambda.\] Adnabyddir problem o'r math yma gydag amodau cychwynnol fel problem Cauchy.
Deillio hafaliad d'Alembert
Datrysiad ar linyn hyd-meidraidd
Mae'r hafaliad ton ar linyn hyd-meidraidd gydag amodau cychwynnol a ffin addas (e.e., terfynau sefydlog) yn enghraifft o broblem Sturm-Liouville. Gellir ei ddatrys trwy ddarganfod datrysiad gwahanadwy ar ffurf \[u(x,t)=X(x)T(t).\] Trwy amnewid y ffurf yma mewn i'r hafaliad differol rhannol ac ad-drefnu, gallwn ostwng y broblem i ddau hafaliad differol cyffredin trefn dau, un ar gyfer \(X(x)\) a'r llall ar gyfer \(T(t)\). Ymddangosir hyn oherwydd bod un ochr yr hafaliad differol cyffredin yn ffwythiant o \(t\) yn unig, a'r llall yn ffwythiant o \(x\) yn unig; gan fod y rhain yn newidynnau annibynnol, mae'n rhaid bod y ddau ochr yn hafal i gysonyn. Wrth ddatrys y broblem ar gyfer \(X(x)\) byddwn yn darganfod, fel arfer, y bodola datrysiadau annistadl ar gyfer gwerthoedd penodol o'r gysonyn blaenorol yn unig. Galwn y fath werthoedd yn werthoedd eigen.
Mae'r egwyddor arsodiad yn ein galluogi i ysgrifennu'r datrysiad ar ffurf cyfres anfeidraidd. Yna gallwn ddefnyddio cyfres Fourier er mwyn pennu cyfernodau yn y datrysiad cyffredinol sy'n galluogi'r amodau cychwynnol i gael eu bodloni.
Gweler eich nodiadau darlithoedd ar gyfer y manylion.
Hafaliad Duhamel - hafaliad ton anhomogenaidd
Rhoir hafaliad ton anhomogenaidd un-dimensiynol fel \[u_{tt}-c^2u_{xx}=h(x,t).\] Mae cynnwys y ffwythiant \(h(x,t)\) yn modelu tardd y tonnau.
Gwelon yn y darlithoedd y rhoir datrysiad yr hafaliad ton anomogenaidd gyda'r amodau cychwynnol homogenaidd \[u(x,0)=0,\]\[u_t(x,0)=0,\] fel \[u(x,t)=\frac{1}{2c}\int\limits_{0}^t\int\limits_{x-c(t-\tau)}^{x+c(t-\tau)}h(y,\tau)\mathrm{d}y\mathrm{d}\tau.\]
Deillio hafaliad Duhamel
Animeiddiadau o ddatrysiadau i'r hafaliad ton homogenaidd
Mae'r animeiddiadau isod yn enghreifftio datrysiadau i'r broblem Cauchy ar gyfer yr hafaliad ton homogenaidd 1-D \[u_{tt}-c^2u_{xx}=0,\] with initial conditions \(u(x,0)=f(x)\) ac \(u_t(x,0)=g(x)\). Fel rydym wedi gweld yn y darlithoedd, rhoddir datrysiadau i'r broblem hyn gan fformiwla d'Alembert: \[u(x,t)=\frac{1}{2}\{f(x-ct)+f(x+ct)\}+\frac{1}{2c}\int\limits_{x-ct}^{x+ct}g(\lambda)\mathrm{d}\lambda.\]
Ym mhob achos sydd wedi'i blotio isod, mae \(c=1\).
Plotiau syml o ddatrysiad d'Alembert
Os hoffech roi cynnig arni i wneud rhai eich hunain, cliciwch ar gyfer y cod Python.
Y ffwythiant Gaussaidd (\(e^{-x^2}\)) dadleoliad cychwynnol, cyflymder cychwynnol yn sero

Ffordd arall i blotio yr union un ffwythiant o \(x\) a \(t\) yw plot arwyneb:

Nodwch y tebygrwydd rhwng y plot hyn a'r brasluniau rydym wedi lluniadu yn y darlithoedd pan yn trafod syniadau sy'n berthynol i achosiaeth.
Y ffwythiant Gaussaidd (\(e^{-x^2}\)) dadleoliad cychwynnol, cyflymder cychwynnol sinwsoidaidd (\(\frac{1}{10}\sin x\))

Adlewyrchiad
Tybiwch ein bod eisiau datrys yr hafaliad ton ar linyn hanner-anfeidraidd ar \(x>0\), gyda dadleoliad cychwynnol \(u(x,0)=f(x)=e^{-5(x-2)^2}\) a chyflymder cychwynnol \(u_t(x,0)=g(x)=0\). Ar ddiwedd y llinyn (\(x=0\)), rydym yn gosod y dadleoliad yn sero, felly \(u(0,t)=0\) ar gyfer pob \(t>0\).
Rydym wedi gweld yn y darlithoedd bod y ffordd i ddelio gyda'r broblem yma yw od-adlewyrchiad, lle rydym yn estynu'r amodau cychwynnol trwy eu hadlewyrchu mewn modd od fel eu bod wedi'u diffinio ar gyfer pob \(x\in\mathbb{R}\).
Dangosir hyn yn yr animeiddiad isod. Llun o'r amod cychwynnol yw'r ffram gyntaf, felly gallwch weld yr od-adlewyrchiad yn glir.

Dyma'r animeddiad os gadawn i amser i redeg:

Y datrysiad i'r broblem gwreiddiol yw cyfyngiad y datrysiad i \(x\) bositif, h.y. popeth i'r dde o'r llinell coch. Mae popeth i'r chwith o'r llinell coch yn declun fathemategol yn unig, sy'n ein galluogi i ddefnyddio fformiwla d'Alembert. Mae natur od yr adlewyrchiad yn sicrhau bod yr amod ffin ar ddiweddbwynt y llinyn yn cael ei fodloni.