Candidate solutions to partition problems with least perimeter

candidates for N=32

Monodisperse case

This PDF document gives (mostly conjectured) minimizers for several classes of equal area isoperimetric/packing problems in two and three dimensions, in some sense generalizing the celebrated Honeycomb Conjecture for the tiling of the plane proved by Hales. These cover:

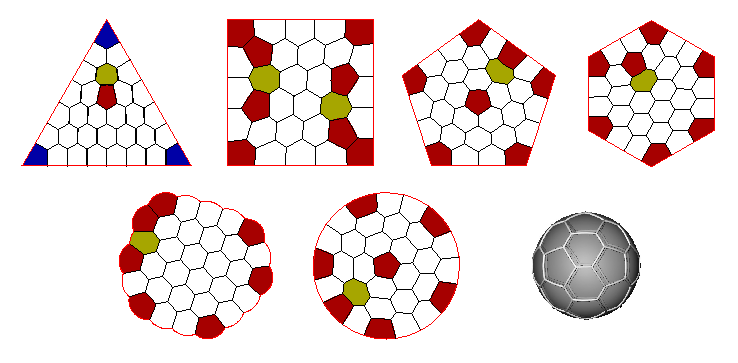
Minimal perimeter enclosing N cells of equal area (N ≤ 42).
Minimal perimeter partition of the disk, the equilateral triangle, the square, the regular pentagon and the regular hexagon into N cells of equal area (N ≤ 42).
Minimal perimeter partition of the surface of the sphere (N ≤ 32).

For a number of larger values of N, particularly powers of 10 and hexagonal numbers, this PDF document gives conjectured minimizers for the minimal perimeter enclosing N cells of equal area.

Please tell me if you find something better, or if you think I have inadequately or incorrectly attributed results.

See the 4th edition of Frank Morgan's book, Geometric measure theory: a beginner's guide (Academic Press, 2009), to find out why these problems are interesting and the mathematics behind them.

All solutions were calculated with Brakke's Surface Evolver. Further details about the calculations can be found in

S.J. Cox, F. Graner, M.F. Vaz, C. Monnereau-Pittet and N. Pittet (2003) Minimal perimeter for N identical bubbles in two-dimensions: calculations and simulations. Phil. Mag. 83:1393-1406.
S.J. Cox (2006) Calculations of the minimal perimeter for N deformable cells of equal area confined in a circle. Phil. Mag. Letts. 86:569-578.
S.J. Cox and E. Flikkema (2010) The minimal perimeter for N confined deformable bubbles of equal area. Elec. J. Combinatorics 17:R45.
S.J. Cox, F. Morgan and F. Graner (2013) Are large perimeter-minimizing two-dimensional clusters of equal-area bubbles hexagonal or circular? Proc. Roy. Soc A 469: 20120392.

Bidisperse case

Here are conjectured minimizers for patterns in which bubbles take one of two possible areas:

Free clusters: The minimal perimeter enclosing N/2 cells of area A=2 and N/2 cells of area A=1, for N=4,6,8 and 10. Conjectured least perimeters are, respectively, 13.512852, 19.050002, 24.400859 and 29.693421.
For details see Vaz, M.F., Cox, S.J. and Alonso, M.D. (2004) Minimum energy configurations of small bidisperse bubble clusters. J. Phys: Condensed Matter, 16:4165-4175.
Confined clusters: this article (F.J. Headley and S.J. Cox (2019) Euro. Phys. J. E. 42: 92.) describes an exhaustive method to generate conjectured minimizers for the least-perimeter partition of the disc into N ≤ 10 regions of two different areas, for all area ratios. The conjectured minimizers are illustrated here and an example of a Surface Evolver file is available here.
Space-filling 2D foams: bidisperse tilings of the plane, with equal numbers of bubbles of each of two areas and small unit cells, have been catalogued by M.A. Fortes and P.I.C. Teixeira: Minimum perimeter partitions of the plane into equal numbers of regions of two different areas, Eur. Phys. J. E, 6:133-137, 2001.

Polydisperse free clusters

Conjectures for the minimal perimeter enclosing N cells with areas 1 to N are given in this PDF document for N up to 50. Again, please tell me if you find something better, or if you know of exact results.

Back to main page and contact details