Mathemateg Tynnu Calonnau

English

Mathemateg Tynnu Calonnau

Yn y gweithdy hwn, byddwn yn dysgu sut i dynnu llun calonnau gan ddefnyddio amryw sgiliau mathemategol mwyfwy anodd.

Cliciwch ar deitl eich lefel ddewisiedig i ddatgelu'r heriau, a gweld pa mor bell y gallwch wthio eich hun.

Lefel Anhawster: Cynradd

Rhaid defnyddio gwahanol siapiau i bob un o'r heriau isod. Mae'r templedau ar gyfer pob un o'r rhain yn ein pdf Templedau Cynradd


Her 1:

Allwch chi greu calon gan ddefnyddio'r siapiau hyn?

Sgwâr a dau hanner cylch. Mae ochr syth pob hanner cylch yr un hyd ag un ochr y sgwâr
Awgrym:

Cylchdrowch y sgwâr i orwedd ar un pwynt fel hyn:

Y sgwâr wedi ei chylchdroi i edrych fel diemwnt

Ateb:
Y sgwâr wedi ei chylchdroi i edrych fel diemwnt. Yna, gosodir ymylon syth y ddau hanner cylch ar hyd ddwy ochr uchaf y diemwnt. Yr effaith a grëir yw cynllun calon sy'n hawdd i'w adnabod.

Her 2:

Allwch chi greu calon gan ddefnyddio'r siapiau hyn?

Dau driongl ongl sgwâr unfath a dau hanner cylch unfath. Mae ymylon syth yr hanner cylchoedd yr un hyd ag ochr fyrraf y trionglau

Awgrym:

Dechreuwch trwy baru ochr syth hanner cylch ag ochr o'r un hyd ar driongl


Ateb:
Mae ymylon syth yr hanner cylchoedd yn cael eu gosod ar ochr y triongl sy'n cyfateb iddynt o ran ei hyd. Mae'r rhain yn ffurfio llinellau crymion uchaf siâp calon a gellir paru ochrau'r triongl i ffurfio triongl isosgeles.

Her 3:

Allwch chi greu cynllun tebyg i galon gan ddefnyddio'r siapiau hyn?

Hanner cylch mawr a dau hanner cylch unfath llai. Mae gan yr hanner cylchoedd llai ymyl syth sydd hanner hyd yr ymyl ar yr hanner cylch mwy.

Awgrym:

Un ymyl syth yn unig sydd gan bob siâp yn yr her yma. Rhaid i'r ymylon syth orwedd yn erbyn ei gilydd.


Ateb:
Mae'r hanner cylch mwyaf yn cynrychioli hanner isaf cylch ac mae'r ddau hanner cylch llai yn gorwedd ar y top, ac yn cwrdd hanner ffordd.

Gweithgaredd Plethu Calonnau

Er mwyn ychwanegu elfen o hwyl i'r ymarfer, rydym wedi cynnwys y cyfarwyddiadau hyn ar gyfer creu eich cynlluniau calonnau plethedig eich hunain.

Mae'r ddau dempled yma wedi eu ffurfio o sgwâr â hanner cylch sydd ynghlwm wrth hyd llawn un ymyl. Mae llinell ddi-dor yn dynodi'r ochr sy'n uno. Mae gwahanodau ('dashed lines') yn rhannu'r sgwâr yn 10 colofn o'r ymyl sy'n uno at ochr y sgwâr sydd gyferbyn.

Gallwch un ai dynnu llun eich fersiwn chi o'r siapiau hyn neu ddefnyddio ein templedau printiadwy ar gyfer calonnau plethedig.

Rydym yn argymell eich bod yn defnyddio cerdyn yn hytrach na phapur er mwyn osgoi rhwygo ar ddamwain.

Gan fod defnyddio siswrn yn rhan o'r gweithgaredd hwn, gwnewch yn sicr fod oedolyn cyfrifol yn eich goruchwylio.

Rhaid ichi dorri'r ddau siâp o amgylch yr amlinelliad cyfan - Peidiwch â thorri'r llinell ddi-dor sy'n mynd trwy'r siapiau.

Nawr, torrwch ar hyd bob un o'r gwahanodau hyd at y llinell ddi-dor.

Plethwch yr edefynnau gyda'i gilydd, yn ofalus, fel y dangosir yn y lluniau isod:

templedau'r galon ar ôl i'r edefyn glas cyntaf gael ei blethu ar draws yr un coch
templedau'r galon ar ôl i'r ail edefyn glas gael ei blethu ar draws yr un coch

Ar ôl ei gwblhau, fe ddylai edrych yn debyg i hyn:

cynlllun calon blethedig wedi ei gwblhau

Awgrymiadau: Gallech ddefnyddio clipiau papurau i ddal yr edefynnau yn eu lle tan i chi eu cwblhau. Gallwch hefyd ddefnyddio tâp clir ar y cefn i'w ddal mewn lle.

Chwilio am ragor i'w wneud? Rhowch gynnig ar wahanol liwiau, meintiau a niferoedd edefynnau.


Lefel Anhawster: Uwchradd

Cynlluniwyd yr heriau hyn i brofi eich gwybodaeth am ddisgrifiadau siapiau a llinellau.

Bydd angen pensel, pren mesur, onglydd a chwmpawd tynnu llun, arnoch.


Her 4:

Dilynwch y cyfarwyddiadau hyn:

  1. Tynnwch lun triongl isosgeles yn sefyll ar ei bwynt. Dylai fod yn 5cm o led a 7cm o uchder.

    Ateb:
    triongl â pharamedrau i gyflawni'r cam hwn

  2. Enwch y pwyntiau ar y llinell lorweddol yn A (ar y chwith) a B (ar y dde), a'r pwynt ar ei waelod yw C

  3. O bwynt A, tynnwch linell 5cm berpendicwlar i linell AC tuag at i fyny.

    Awgrym:

    Beth yw ystyr perpendicwlar?

    Er mwyn bod yn berpendicwlar i linell, rhaid bod ar onglau sgwâr (90°) iddi


    Ateb:
    llinell a ychwanegwyd at y triongl blaenorol o bwynt A, ar ongl 90° i'r llinell AC.

  4. O bwynt B, tynnwch linell berpendicwlar i linell BC, mae'n croesi'r llinell a dynnwyd yn y cam blaenorol ar bwynt D

    Ateb:
    Y triongl a ffurfiwyd trwy ychwanegu pwynt D

  5. Gan ddefnyddio cwmpawd, tynnwch lun arc, gyda'r cloc, o bwynt A i D

    Awgrym:

    Beth yw arc?

    Rhan o gylchedd (ymyl) cylch yw arc.

    Sut mae gosod y cwmpawd ar gyfer yr arc hwn?

    Dylai pigyn y cwmpawd fod yng nghanol y cylch, a fydd yng nghanol llinell AD.

    Dylid agor y cwmpawd er mwyn i'r pensel ddechrau ar bwynt A.


    Ateb:
    Ychwanegu arc hanner cylchol sy'n uno pwyntiau A a D

  6. Gan ddefnyddio cwmpawd, tynnwch lun arc, yn groes i'r cloc, o bwynt B i D

    Ateb:
    Ychwanegu ail arc hanner cylchol sy'n uno pwyntiau B a D

Her 5:

Dilynwch y cyfarwyddiadau hyn:

  1. Tynnwch linell lorweddol 5cm

  2. Marciwch un pwynt terfyn yn A a'r pwynt arall yn B

  3. Gan ddefnyddio pwynt A fel y canol, tynnwch lun cylch gyda radiws o 2.5cm

    Awgrym:

    Beth yw radiws cylch?

    Y radiws yw'r pellter rhwng canol y cylch ac unrhyw bwynt ar yr arc/cylchedd.

    Tri chylch, a chanddynt linell bob un sy'n uno'r canol â gwahanol rannau o arc/cylchedd y cylch

    Ateb:
    Cylch â radiws o 2.5cm a llinell lorweddol 5cm o'i ganol ac allan i'r dde.

  4. Gan ddefnyddio pwynt B fel y canol, tynnwch lun cylch â diamedr o 5cm

    Awgrym:

    Beth yw diamedr cylch?

    Y diamedr yw'r pellter rhwng pwyntiau cyferbyn ar arc/cylchedd cylch.

    Tri chylch, a chanddynt linell bob un sy'n uno dau wahanol bwynt cyferbyn ar eu harcau/cylcheddau

    Ateb:
    Dau gylch unfath a'u canol ym mhob pen i linell lorweddol, ac yn cyffwrdd yng nghanol y llinell.

  5. Yn y man lle mae'r ddau gylch yn cwrdd, tynnwch linell syth tuag at i lawr 7cm. Diwedd y llinell yw pwynt C

    Ateb:
    Dau gylch unfath a'u canol ym mhob pen i linell lorweddol, ac yn cyffwrdd yng nghanol y llinell. Mae llinell 7cm ychwanegol yn mynd tuag at i lawr yn fertigol o ganol llinell AB (lle mae'r cylchoedd yn cwrdd)

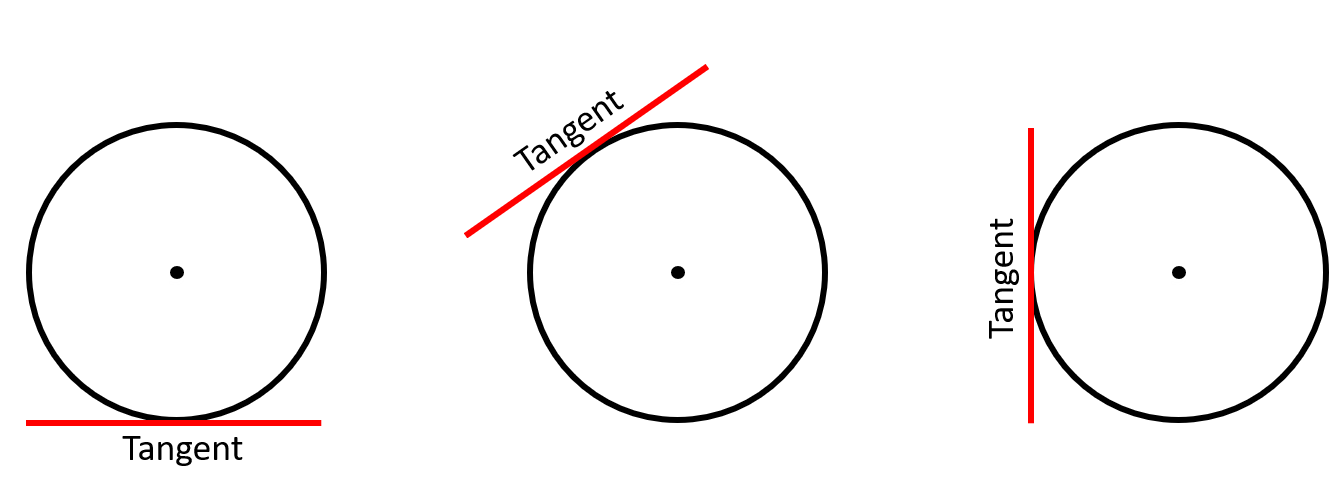
  6. Tynnwch lun y llinell dangiad ar gyfer pob cylch a fydd yn cysylltu â phwynt C

    Awgrym:

    Beth yw llinell dangiad?

    Tangiad cylch yw unrhyw linell syth sy'n cyffwrdd ymyl cylch heb basio trwy arc y cylch.

    Tri chylch, a chanddynt linell syth bob un sy'n cyffwrdd â man gwahanol ar arc/cylchedd y cylch

    Ateb:
    Dau gylch unfath, a'u canol ym mhob pen i linell orweddol, ac yn cyffwrdd yng nghanol y llinell. Mae llinell 7cm yn mynd tuag at i lawr yn fertigol o ganol llinell AB (lle mae'r cylchoedd yn cwrdd). Ychwanegwyd dwy linell arall o bwynt C, un ar gyfer pob un o'r cylchoedd ac yn cysylltu ar dangiad

Her 6:

Dilynwch y cyfarwyddiadau hyn:

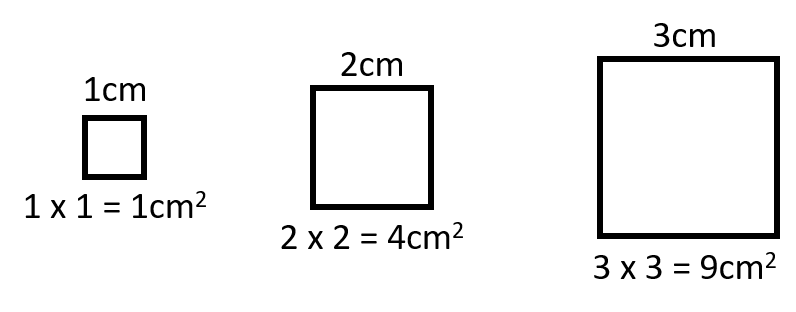
  1. Tynnwch lun sgwâr a chanddi arwynebedd 36cm2

    Awgrym:

    Sut mae gweithio allan hyd yr ochrau?

    Arwynebedd unrhyw sgwâr neu betrayal = lled × uchder.

    Yr un lled ac uchder sydd i sgwâr

    Tair sgwâr, mae ochrau'r gyntaf 1cm o hyd ac mae ganddi felly arwynebedd o 1cm sgwâr, mae ochrau'r ail yn 2cm ac mae ganddi felly arwynebedd o 2 × 2 = 4 cm sgwâr, ac mae ochrau'r drydedd yn 3cm ac arwynebedd = 3 × 3 = 9 cm sgwâr

    Ateb:
    Sgwâr a chanddi ochrau 6cm o hyd

  2. Labelwch y corneli yn A, B, C a D, i gyfeiriad y cloc, gydag A ar y chwith uchaf.

  3. Tynnwch lun cylch a chanddo ddiamedr 6cm, a phwynt A yw'r canol

    Awgrym:

    Beth yw diamedr cylch?

    Diamedr yw'r pellter rhwng pwyntiau cyferbyn ar arc/cylchedd cylch.

    Tri chylch, a chanddynt linell bob un sy'n cyffwrdd â dau wahanol bwynt cyferbyn ar eu harcau/cylcheddau

    Ateb:
    Sgwâr a chylch o led hafal yn gorgyffwrdd, â chanol y cylch ar gornel chwith uchaf y sgwâr

  4. Ailadroddwch y cam diwethaf gan ddefnyddio pwyntiau B, C a D fel y canol

    Ateb:
    Sgwâr a phedwar cylch o led hafal yn gorgyffwrdd, â chanol pob cylch ar un o gorneli'r sgwâr

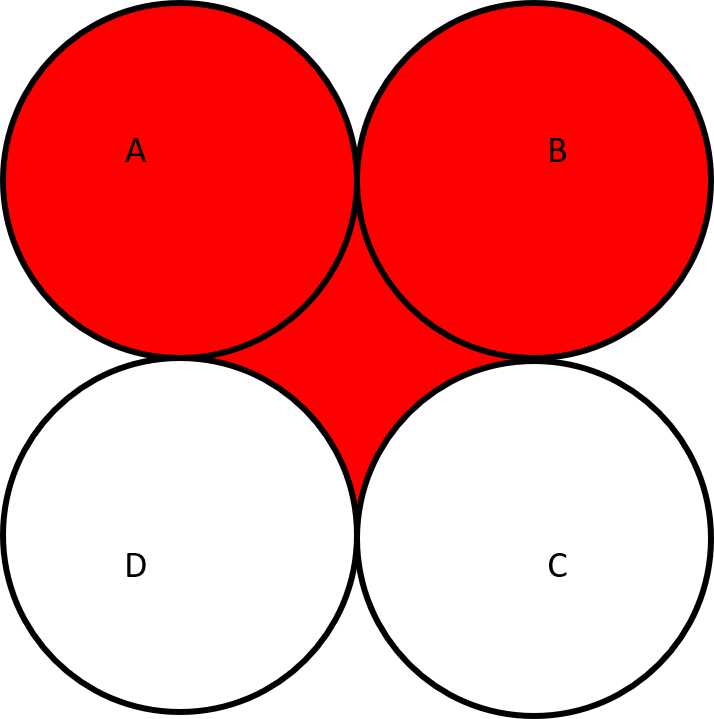
  5. Gan ddefnyddio pen/pensel coch, lliwich y cylchoedd sy'n amgylchynu pwyntiau A a B

    Ateb:
    Siapiau a chynllun y cam blaenorol, gyda'r ddau gylch uchaf wedi eu huwcholeuo

  6. Gyda'r un pen/pensel coch, lliwiwch y siâp a ffurfiwyd y tu mewn i'r sgwâr gan arcau'r pedwar cylch

    Ateb:
    Yr un siapiau a chynllun â'r cam blaenorol, gyda'r siâp a ffurfir y tu mewn i'r sgwâr gan arcau'r pedwar gwahanol gylch hefyd yn cael ei uwcholeuo - mae'r ardaloedd a uwcholeuir nawr yn dangos amrywiad ar gynllun calon

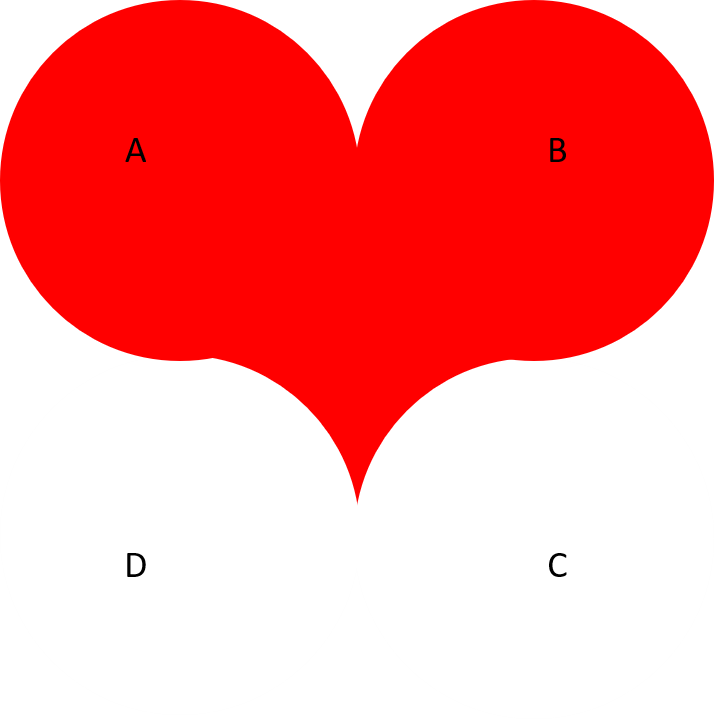
    Er mwyn helpu i ddangos cynllun terfynol calon, rydym wedi dileu amlinelliad y siapiau yn y fersiwn isod:

    Y cynllun uchod ond gydag amlinelliad y sgwâr a'r ddau gynllun isaf wedi eu dileu, gan adael siâp calon yn unig


Ar gyfer y detholiad nesaf o heriau, bydd angen defnyddio siswrn, glud a thâp.

Her 7:

  1. Estynnwch ddarn A4 o bapur neu gerdyn.

  2. Torrwch stribed 2cm o led.

  3. Defnyddiwch y stribed hwn o bapur (sydd â dwy ochr), a cheisiwch greu siâp unochrog.

Ni fydd yn rhaid i chi ddefnyddio siswrn, ond bydd angen tâp arnoch.

Awgrym:

Onid yw'n amhosib? Bydd dwy ochr i'r papur o hyd.

Mae'n bosib. Ceir 'tro' annisgwyl i'r her wrth dapio'r ddau ben at ei gilydd.


Ateb:

Er mwyn creu siâp unochrog, tapiwch y papur mewn dolen trwy ei droi unwaith yn unig. I'w brofi, mynnwch ben neu bensel a thynnwch linell ar hyd canol y stribed - dylai uno heb gael ei dynnu o'r papur, gan brofi ei fod yn unochrog.

Stribed o gerdyn a'i ddau ben wedi eu tapio gyda'i gilydd er mwyn ffurfio dolen ac ynddi un troad

Her 8:

Gelwir y siâp unochrog hwn yn Stribed Môbius.

  1. Un ai crëwch Stribed Môbius neu ddefnyddio'r un o her 7, tynnwch linell i lawr y canol.

    Datgelwch y Llun
    Stribed o gerdyn â'i ddau ben wedi eu tapio gyda'i gilydd i ffurfio dolen ac ynddi un troad. Marciwyd llinell ar hyd canol y stribed.

  2. Pa siâp/siapiau fyddai'n cael eu creu pe bawn ni'n torri ar hyd y llinell hon? Ystyriwch, ond peidiwch â gwneud hyn eto.

  3. Meddyliwch am (neu hyd yn oed arbrofwch gyda) beth fyddai'n digwydd pe baech yn torri dolen syml (heb droadau) o bapur ar hyd y llinell yn y canol.

  4. Gadewch inni ganfod yr ateb. Torrwch eich Stribed Môbius ar hyd y llinell yn y canol.

  5. Pa siâp/siapiau sydd gennych? Sawl ochr?

    Ateb:

    Mae gennym bellach ddolen ddwyochrog (ymyl tu mewn a thu allan) ac ynddi bedwar troad!

    Dolen fwy â 4 troad

  6. Sawl troad sydd yn y siâp/siapiau? Gallwch wirio hyn trwy dorri trwy'r stribed a chyfrif sawl gwaith y mae'n rhaid i chi droi'r papur i'w ddatod.

Her 9:

  1. Mynnwch ddau stribed newydd o gerdyn neu bapur o'r un maint a'u gludo gyda'i gilydd ar ffurf croes.

    Datgelwch y Llun
    Dau stribed o gerdyn wedi eu gludo yn y canol i ffurfio croes

  2. Tapiwch un o'r stribedi hyn yn ddolen syml, a'r llall yn Stribed Môbius.

    Datgelwch y Llun
    Dolen syml o gerdyn du wedi ei chlymu ar ongl sgwâr i Stribed Môbius.

  3. Torrwch ar hyd llinell ganolog y ddau, ond nid ar hyd y darn sy'n uno'r ddau.

    Datgelwch y Llun
    Dolen syml o gerdyn du wedi ei chlymu ar ongl sgwâr i Stribed Môbius. Torrwyd y ddau ar hyd llinellau canol y stribedi oddi amgylch y mannau lle maen nhw'n wedi eu clymu at ei gilydd.

  4. Cyn inni gwblhau'r toriadau ar draws yr ardal sydd wedi ei gludo, meddyliwch am ba siâp/siapiau y bydd gwneud hyn yn eu creu.

    Gwyddom o'r her flaenorol beth ddigwyddodd gyda Stribed Môbius yn unig, a gwyddom y bydd torri un ddolen syml ar hyd y llinell yn y canol yn creu dwy ddolen.

  5. Pan rydych yn barod i gadarnhau eich rhagfynegiadau/meddyliau, cwblhewch y toriadau trwy'r ardal olaf - bydd yn rhaid ichi eu dal yn eu lle rhwng y ddau doriad.

    Ateb:

    Mae gennym sgwâr!

    Ffrâm sgwâr o stribedi cerdyn

Ai dyma beth roeddech chi'n ei ddisgwyl?

Her 10:

  1. Gyda dau stribed newydd o bapur/cerdyn, gludwch nhw gyda'i gilydd ar yr un ffurf croes ag yng ngham 1 her 9

  2. Y tro hwn, byddwn yn tapio'r ddau fel Stribedi Môbius gyda throadau dirgroes. Mae hynny'n golygu y bydd y naill yn cael ei droi gyda'r cloc cyn ei dapio, a'r llall i gyfeiriad gwrthglocwedd.

    Datgelwch y Llun
    Dau Stribed Môbius o'r un hyd yn union a chyfeiriadau troi dirgroes wedi eu clymu ar onglau sgwâr i'w gilydd

  3. Torrwch ar hyd llinellau canol pob stribed, hyd at ochrau'r ardal sy'n eu huno, ond nid trwy'r ardal honno

    Datgelwch y Llun
    Dau Stribed Môbius o'r un hyd yn union a chyfeiriadau troi dirgroes wedi eu clymu ar onglau sgwâr i'w gilydd. Torrwyd y ddau ar hyd llinellau canol y stribedi, hyd at ochrau'r ardal sy'n eu huno, ond nid trwy'r ardal honno.

  4. Cyn inni gwblhau'r toriadau canolog ar hyd yr ardal sy'n eu huno, beth am inni ystyried beth allai ddigwydd y tro hwn.

  5. Pan rydych yn barod, cwblhewch y toriadau i weld pa mor gywir yw eich rhagfynegiadau.

    Ateb:

    Mae gennym bellach ddwy galon wedi eu cyd-gloi.

    Dau siâp calon wedi eu cyd-gloi

Awgrym: Os oes gennych ddau siâp ar wahân ar yr adeg yma, mae'n golygu eich bod wedi troi'r ddau Stribed Môbius i'r un cyfeiriad, ac nid i gyfeiriadau gwahanol (fel y gofynnwyd ichi ei wneud yng ngham 2).


Lefel Anhawster: Safon Uwch

Her 11:

Dilynwch y cyfarwyddiadau isod:

  1. Tynnwch lun graff \[f(x) = \sin(x)\] ar gyfer \[0 < x <{\pi \over 2}\]

    Ateb:
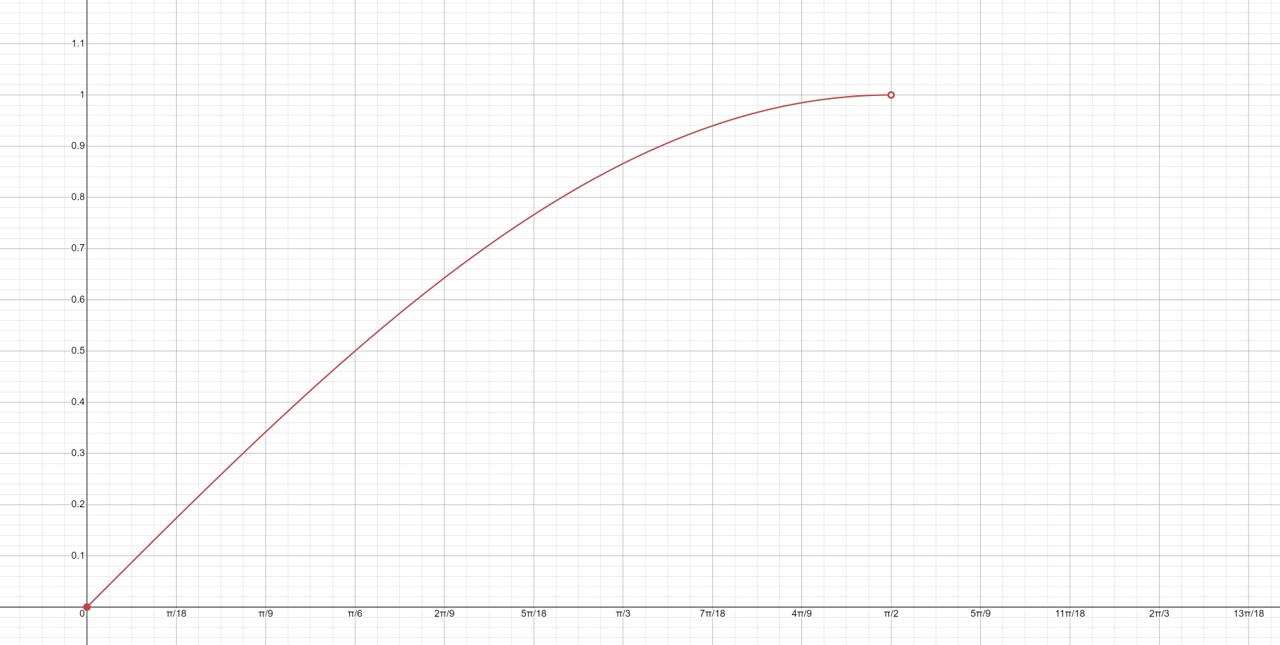
    Y graff ar gyfer yr hafaliad uchod.

    Cynhyrchwyd y graff gan ddefnyddio offeryn datrys problemau sydd ar gael ar Mathway.com

  2. Cylchdrowch y cromlin a gynhyrchwyd -90°

  3. Tynnwch lun adlewyrchiad y cromlin hwn, yn cyffwrdd yn y gwaelod

  4. Tynnwch linell lorweddol ar hyd y top i ffurfio triongl a chanddo ddau gromlin ac un ochr syth.

    Ateb:
    Triongl a ffurfiwyd o'r llinell graff uchod, ei hadlewyrchiad a llinell lorweddol

  5. Marciwch ben chwith y llinell orweddol hon yn bwynt A, y pen dde yn bwynt B a'r pwynt canol yn C

  6. Tynnwch lun arc 180° sy'n uno pwynt A a phwynt C mewn cyfeiriad clocwedd, ac ailadroddwch hyn i uno pwynt C a phwynt B

    Ateb:
    A combination of the above to form a shape recognisable as a heart symbol

Her 12:

Dilynwch y cyfarwyddiadau isod:

  1. Tynnwch lun graff \[f(x) = \sin(x)\] ar gyfer \[-{\pi \over 2} < x < {\pi \over 2}\]

    Ateb:
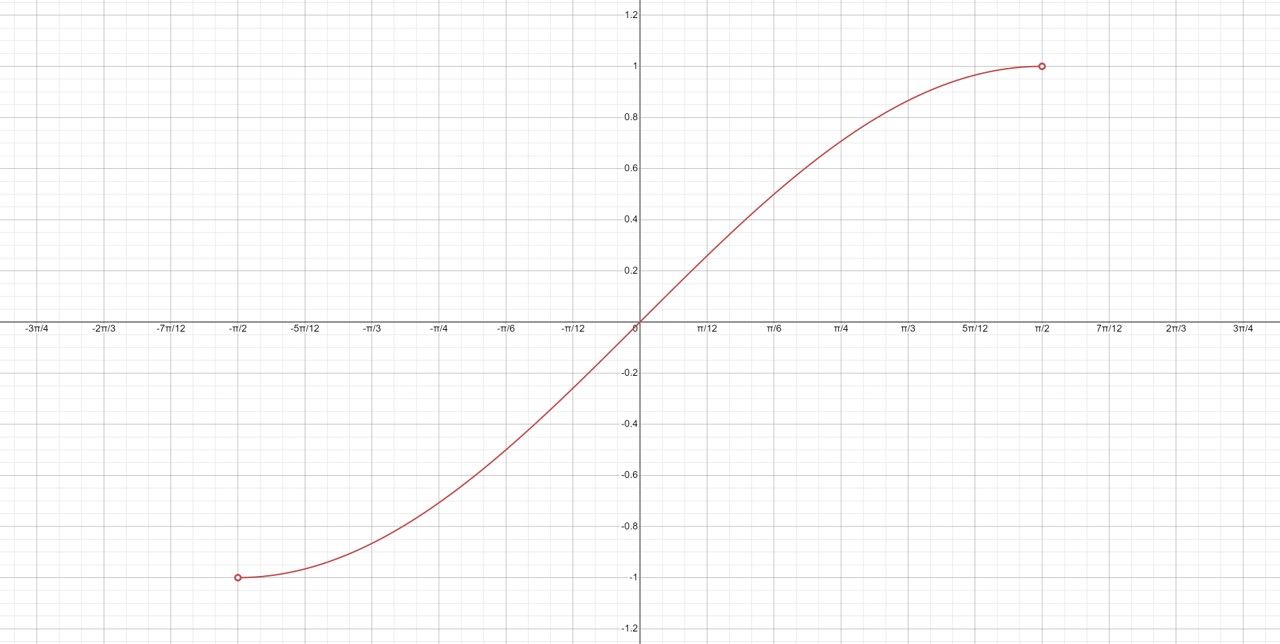
    Y graff ar gyfer yr hafaliad uchod.

    Cynhyrchwyd y graff gan ddefnyddio offeryn datrys problemau sydd ar gael ar Mathway.com

  2. Cylchdrowch y cromlin a gynhyrchwyd -90°

  3. Tynnwch lun adlewyrchiad y cromlin hwn, yn cyffwrdd yn y gwaelod

  4. Tynnwch linell lorweddol ar hyd y top i ffurfio triongl a chanddo ddau gromlin ac un ochr syth.

  5. Marciwch ben chwith y llinell orweddol hon yn bwynt A, y pen dde yn bwynt B a'r pwynt canol yn C

  6. Tynnwch lun arc 180° sy'n uno pwynt A a phwynt C mewn cyfeiriad clocwedd, ac ailadroddwch hyn i uno pwynt C a phwynt B

    Ateb:
    Cyfuniad o'r uchod i ffurfio siâp y gellir ei adnabod fel symbol calon

Her 13:

Dilynwch y cyfarwyddiadau isod:

  1. Tynnwch lun graff gan ddefnyddio'r hafaliadau parametrig \[x = \alpha \cos t (1 - \cos t)\] a \[y = \alpha \sin t (1 - \cos t)\]

  2. Chylchdrowch y cromlin a gynhyrchwyd o -90°

    Ateb:
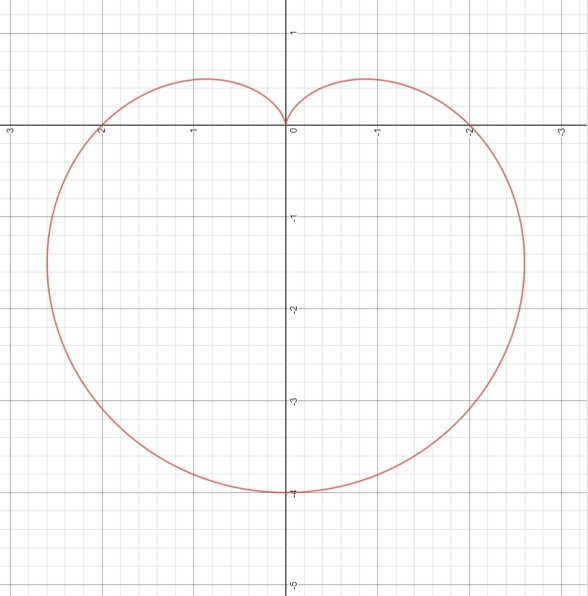
    Cardioid - neu gynrycholiad crwm iawn o galon.

    Cynhyrchwyd y graff hwn ar Gyfrifiannell Desmos.com ddefnyddio'r hafaliad polar ar gyfer y cromlin hwn

Gelwir y siâp hwn yn gardioid (daw cardio o'r Groeg ar gyfer 'y galon'). Mae'n fwy crwm na'r cynlluniau arferol sydd gennym ar gyfer calon.

Gellir creu cardioidau yn naturiol, er enghraifft trwy adlewyrchiad golau mewn cylch.

Y cardioid hefyd yw prif ffigwr y set Mandelbrot.


Gweithgaredd Estynedig

Mae gweithdy arall ar thema ramantus ar lein o'r enw Blodau Crwban. Nod y gweithdy hwn yw tynnu llun blodau trwy ddilyn cyfarwyddiadau rhaglennu.

Ceisiwch ddefnyddio'r un rhaglen i ailgynhyrchu'n gywir yr holl gynlluniau calon rydych wedi eu creu yma.


Adnoddau Ychwanegol

Os oes gennych ddiddordeb mewn dysgu mwy am y fathemateg y tu ôl i'r calonnau, edrychwch ar y gwefannau canlynol: