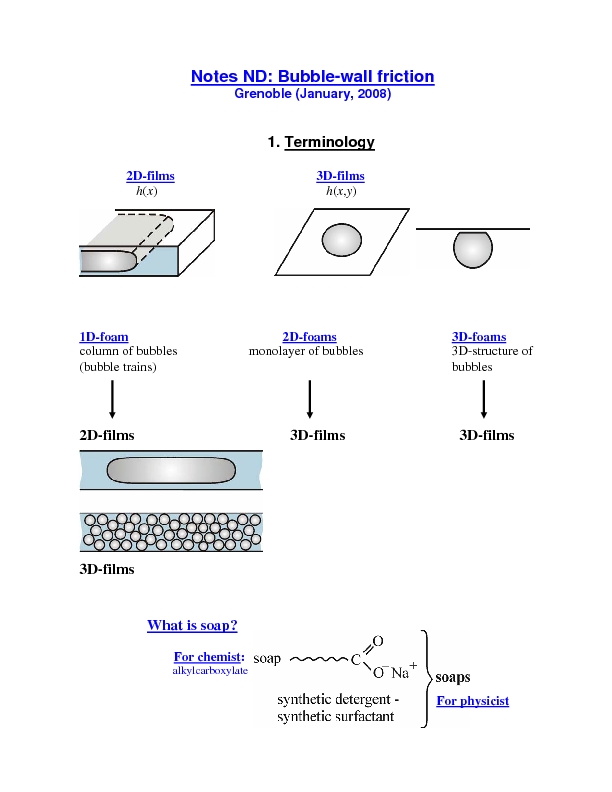





10h Preparation of planning
11h30 Presentation of debate : Wall friction - Notes by N. Denkov
14h Lab seminar : M. Dennin
15h Localization - Notes by R. Hohler?
16h Couette shear - Notes by A. Wyn and summary of published
work
17h Drainage and convective instability - Notes by G. Thomas
9h Private discussions
10h G' and G" versus frequency and amplitude - Notes by F. Elias
11h30 Presentation of debate : Localization - Notes by R. Höhler
14h Five-minutes presentations
14h Microfluidics - Notes by A. Mughal
15h Private discussions
16h Bubble interaction at the bubble level - Notes by XXX
17h Screening of a perturbation - Notes by J. Lambert
18h Wall dissipation - Notes by XXX
9h30 Surface Evolver tutorial
9h30 Foam acoustics - Notes by B. Dollet
10h Private discussions
11h30 Presentation of debate : liquid fraction - Notes by A. Saint-Jalmes and B. Dollet
13h30 Coarsening of wet foams - Notes by C. Gay
14h Five-minutes presentations
15h Visco-elasto-plastic models - Notes by J. Barry
16h Liquid fraction - Notes by A. Saint-Jalmes
16h Conformal crystals - Notes by J. Barry
17h Scalar measures of disorder - Notes by G. Katgert
18h Potts model tutorial
9h Parallel plate compression of foams and cells - Notes by S. Cox
10h Stokes experiment - Notes by I.T. Davies
and summary of published
work
11h Dilatancy - Notes by C. Gay
11h30 Presentation of debate : Plasticity, yielding, T1s - Notes by I. Cantat
13h30 Private discussions
14h Five-minutes presentations
15h Private discussions
16h Matrix measures of disorder - Notes by F. Graner
17h Effect of disorder on foam properties - Notes by C. Gay
18h Private discussions
9h30 Emulsions - Notes by XXX
10h Real 3D structure of quasi-2D foams - Notes by I.T. Davies
11h30 Presentation of debate : Constitutive equations - Notes by P. Marmottant
13h30 Dilatancy - Notes by C. Gay
14h Feedback on the workshop - Notes by F. Graner
15h Overshoot - Notes by M. Dennin
16h Jamming transition - Notes by S. Cox
17h Private discussion
18h Foam experiments in beer bar
Couette = any flow which is driven by the boundary Different types: LG - liquid glass, LA - liquid air, GG - glass glass, LM - Langmuir monolayers Linear Couette, Cylindrical Couette, Pure Shear, Periodic B.C. Parameters 2D/3D, Polydisperse, Exp/Sim/Theory, liquid fraction, confinement, strain rate, composition. Many different studies, therefore many different geometries. Are there any common things that can be compared? How do we compare them? Enough parameter space in experiments to account for different results. Not necessarily a contradiction as yet. We should only compare data from the same regimes. Even when using the same regimes, can we have common dimensionless parameters? What should they be?
Drainage and convective instability, Monday 17h
G' and G" versus frequency and amplitude, Tuesday 10h
1) What is the relation between the following 5 types of experiments. Are the same generic mechanisms involved or not ? A) 2D foam with significant extrinsic friction B) 2D foam without significant extrinsic friction C) 3D foam D) 3D emulsions (with or without attractive droplet interactions). E) Confined foams and emulsions 2) Are there within one of these 5 categories conditions which clearly induce or inhibit localization ? (Examples: liquid fraction in 3D foam, droplet attraction in emulsions...) 3)The Herschel Bulkley Model does not allow to take into account localization. Still, it is widely used and may be a good approximation under certain conditions. Which are exactly these conditions ? 4) Examples of power-law behavior with critical strain rate have been evidenced in B) and C), even though the critical strain rate is a robust quantity only under certain conditions in B). Which features of the sample or the experiment set the critical strain rate ? Is there a correlation with yield strain and T1 duration, as proposed by Picard et al. PRE 2005 ? 5) Which is the length scale below which macroscopic descriptions of foam flow break down ? Is the fluidity model by Picard, Lequeux, Ajdari et al a good approach to handle local rheology ? 6) How does localization depend on polydispersity ? Does shear flow induce bubble size segregation, as seen by Herzhaft et al for 3D foam ? 7) How can Visco-elaso-plastic models be adapted by describe heterogeneous flows with minimal strain rate ? Will non-monotonic flow curves come into play ? 8) Simulation techniques. Are there any features that may introduce artifacts in A) The bubble model B) The "standard" surface evolver C) Alexandre Kabla's algorithm 9) Is dynamic dilatancy important for flow localization ? 10) The larger picture: how does flow localization in foams relate to similar phenomena observed in granular materials, pastes etc. Relation with the jamming phase diagram ?
Foam acoustics, Wednesday 9h30
Liquid fraction, Wednesday 11h30
Some general statements :
- is the liquid fraction phi_l an important parameter in foam physics ? Yes
- do we know how the rheological properties depend on phi_l? yes, qualitatively? But, no on a quantitative level.
- what are the origins of this lack of understanding ?
Practical issues : knowing, controlling, measuring liquid fraction is a difficult task. Especially in 2D.
Also, the liquid fraction evolves in time (gravitational drainage, but also gas diffusion coarsening as it
modifies the bubble size and thus the drainage rate.)
Theoretical issues : it is also hard to model foam structure at any liquid fraction.
Two "critical" points : the very dry limit, and the very wet limit. These limits may be easier to model, but more complicated.
- There are strong connection between liquid fraction and disorder and polydispersity.
- All these reasons explain the fact that we still don't know well and quantitatively how the foam rheology depends on phi_l.
- But the situation is not that "bad"? there are some data and model available, valid on given and controlled range of liquid fractions.
There are usually some general agreement between the data from the different groups. But one has also to be careful about the
bubble size and surface tension measurements (since many results are first normalized by the Laplace pressure).
- available models to explain these data ? mostly empirical laws. there are often large discrepancy between the most simple models
(for instance, based on 2D periodic structure) and data. In particular, such comparisons illustrate the crucial role of disorder,
which usually tends to smooth out the sharp variation in the wet or dry limits.
- There are also some coupling between a macroscopic deformation and a liquid fraction gradient. This is related to the dilatancy effect,
and to the shear non-uniformity. A macroscopic deformation can induce liquid displacement inside the liquid network (for instance,
from an unsheared area to a sheared one). Thus, the liquid, even if it was initially uniformly distributed, might be moved by the
deformation. Thus liquid moves inside the structure in response to gravity,
capillarity and macroscopic shear. As well, study of slip at solid surfaces show that some liquid is re-distributed from the Plateau borders
to its adjacent films and nodes during slip. Lastly, a possible origin of shear localisation is the initial existence of a liquid gradient.
Another example of the coupling between rheology and liquid motion inside the structure is the convective instability.
List of rheological quantities depending on liquid fractions :
Viscous drag in 2D
Viscoelastic moduli G' and G"
Yield stress and yield strain
Viscosity and shear stress in steady-shear measurements
Poisson coefficient
Osmotic pressure
(as well as many other non-rheological quantities : electrical, optical, acoustical, etc.. properties)
A more specific issue: fluid fraction in 2D
reminder: exists three main systems (except the "true" 2D foams in Langmuir monolayer):
glass-glass GG, liquid-glass LG and liquid-air LA (bubble raft), see Vaz & Cox, Phil. Mag. Lett. (2005).
only for GG is the liquid fraction unambiguously measurable, as the foam density (measured by weighing) relative to water density.
There is no such possible definition for LG and LA, because the foam naturally exchanges water with a reservoir (open system).
However, one can adjust a "wetness" of a foam by changing the foam thickness in LG (i.e. the distance top plate-bubble bottom)
or by compression in LA. Seen from a 2D top view, the foam then seems more or less, with bigger or smaller vertices.
in simulations: with Evolver, the fluid fraction is implicitely varied by adjusting a cut-off length below which
a bubble edge can no longer exist, then undergoes a T1. In Potts, such a cut-off length is intrinsically set by the lattice parameter/unit mesh size.
in theory: the Decoration Theorem (Bolton & Weaire) is used to model fluid fraction in 2D.
The liquid is assumed to "decorate" the vertices, bounded by arc of circles.
This comparison suggests a common key parameter in all 2D/quasi-2D foam systems: the cut-off length l_c, or the radius of the Plateau
border (Raufaste et al., Eur. Phys. J. E 2007). One could then define an "effective" 2D fluid fraction, valid for all
2D/quasi-2D foams, \Phi_L ~ l_c^2/A, with A the bubble area. Tested on one mechanical quantity (the yield drag),
this definition enables a correct rescaling of data on different systems, exp. (GG, LG), num (Evolver, Potts) and theory.
However, this is not enough, since the real 3D structure of the foam is not correctly taken into account.
First suggestion of improvement: take the surface Sflat of the flat faces through which neighbouring bubbles share a thin film,
since these faces must disappear at the rigidity loss transition and/or when a T1 occurs.
But this fails in highly confined systems, when S_{flat} has a vanishing vertical dimension, although the foam can appear very dry.
Second suggestion of improvement, brought during this workshop (Cantat): the relevant quantity may be the
length L_h of the longest horizontal line drawn on S_{flat}, compared to a relevant bubble dimension ~ \sqrt{A}.
This remains to be tested on different system, with a common measured quantity. Also, the measurement of L_h is not easy in practice;
either it could be measured in the static case by confocal or two-photon microscopy, or determined from structural calculations (Surface Evolver).
Some open questions :
- effective links between theory and experiments : practical and well defined quantity to be measured ?
- can and how the aging (drainage and coarsening) be stopped to study high liquid fractions ?
- what is the best definition of the liquid fraction in 2D and how can it be measured (see above discussion, and also reports on other sessions on this topic) ?
- how can a wet foam be modelled ?
- what are the effect of polydispersity and disorder ? what are the limits of validity of the empirical laws ?
- what is the role of the coupling between macroscopic deformation and liquid displacement ? can such effect be measured ?
- is there a range of liquid fraction for which the shear is always uniform ? or is there a critical phi_l above which, shear localization is always observed ?
- what is the equilibrium between purely interfacial effects and liquid fraction ?
Coarsening of wet foams, Wednesday 13h30
Here, by coarsening we mean the effect of gas diffusion, not film breaking or drainage. What is known: - basic (microscopic) mechanics: diffusion, Laplace pressure, Plateau rules; - 2D dry foam: fate of one bubble area evolution depends on number of sides; - 2D scaling state What is not known: - fate of one bubble? (other than dry 2D) - fate of foam? Self-similar growth (s.s.g.) in dry 2D foam has been known for 50 years: dA/dt \propto (6 - n) where A = area and n = number of sides. "Everybody knows" that any foam goes through a transient and then enters s.s.g., although there is currently no theoretical proof of it. Rita de Almeida has shown, both in 2D and 3D, by minimizing a free energy (interface energy + an entropy constructed on the size distribution), that the size distribution evolves to a particular steady regime. In 3D, there is (approximate) agreement between: Potts simulations (Rita et al recent) Experiments (Jerome unpublished) Simulations (xxxberger) Theory (Rita)
Visco-elasto-plastic models, Wednesday 15h
Liquid fraction, Wednesday 16h
Chairman : M. Dennin Secretary : ASJ Attendance : 10-12 persons Topic : liquid fraction (following the morning speech by ASJ and Dollet) - mostly a discussion on what is the liquid fraction in 2D experiments, how it can be defined or measured, especially for the case of the bubble raft (L.A.) - discussion on which quantities have been measured in 2D as a function of the bubble packing : B. Dollet presents some data on the yield drag. It shows an quasi exponential decay, not fully understood. More generally, it appears that much less is known in 2D than in 3D, concerning how the properties depend on the liquid fraction. Most likely, because this concept is much more difficult to define. Practically speaking, it was noted that for measuring liquid fraction in 2D systems, one have to be careful of how the foam is enlightened : from the side, from below from above? as shown by ray-tracing works, the thickness of black (or white) liquid stripes at the surface can depend strongly on the source distance and position. We also discuss about the use of ?packing fraction? rather than ?liquid fraction? in 2D systems. For the bubble raft, we also discuss about the origin of the elasticity : since the bubble appears spherical, there should be no distortion and no elasticity. An elastic modulus implies a small flat facet between the bubbles. Can this small vertical contact face be visualized or its size measured ? vertical scan using fluorescence microscopy (different in the bulk and in the film) ? two-photon microscopy ?? Lastly, we discuss about what ?Surface Evolver? simulations could provide about the packing of bubbles at the surface of a liquid, with and without top plates. Is there such simulations available? Can they be performed easily ?? M. Dennin also introduce the idea to use Voronoi construction to determine the liquid or packing fraction, once knowing the volume of the bubbles and the position of their center.
Conformal crystals, Wednesday 16h
Parallel plate compression of foams and cells, Thursday 9h
Discussion on the compression of a spherical cluster of cells/bubbles between
parallel plates.
How does aggregate surface tension depend upon adhesion?
Are necessary quantities robust (surface tension, radii of curvature, contact angle)
for cells/foams? Can we calculate them? Can we measure them?
What is the role of elasticity?
The yield stress is very significant (is it measurable, e.g. from the stress on the
plate?): adhesion allows cells to return to a more spherical shape (overcoming yield
stress), which bubbles cannot do when yield stress is high.
for foams: sigma_y = gamma/R f_1(\Phi_l)
for cells: sigma_y = gamma_{eff}/R f_2(temperature?, time?, adhesion?), since
fluctuations allow recovery to spherical shape.
Stokes experiment, Thursday 10h
Introduction to Stokes experiment in foam: What is a Stokes Experiment?
- Object moving relative to a foam. We measure the lift and drag on the obstacle
due to the foam.
- There exists a network force on the obstacle from film tension and a pressure
force from the gas in each bubble.
What is the purpose of the discussion?
To unify data from published work.
Research Group Constant force/velocity Dimension Comparable data
Dublin CF 3D Velocity
Aberystwyth CF 2D Position
Rennes/Marne CV 3D Force, rearrangements
de Bruyn CV 3D Rearrangements
Grenoble (Aber) CV 2D Force
China/Dublin CV 2D Force
Everywhere! CV 3D Rearrangements
Important Parameters
1. obstacle size
2. bubble size
3. liquid fraction (average, gradient, variation)
4. disorder of foam
5. solution composition
6. velocity or force
7. channel width / distance of obstacle to wall
8. obstacle shape
9. boundary conditions
Comparisons suggested during discussion:-
1. Dimensional comparisons, 2D ? 3D
2. Drag force on the obstacle as a function of sphere to bubble size ratio
3. Velocity - (i) along axis of symmetry
(ii) overshoot behind obstacle (scaling exponent of velocity important)
(iii) fluctuations
4. Rearrangements [need to be cautious between 2D and 3D] ? look at the
preferential zones of rearrangements of bubbles (2D case ? Dollet et al)
5. Force fluctuations during foam flow
6. Foam flow in constant force experiments versus foam flow in constant velocity
experiments
7. Experiment (quasi-2D) versus simulation of 2D foams
8. Bubble deformation (the qualitative trends seem interesting, for example the
symmetry of deformations along the centreline axis and variation with the radial
distance from the obstacle)
9. Compare the fields described tensorially for different shaped obstacles,
distance form wall (+ for a foam flow through a constriction)
10. Look at the frequency and orientation of T1s as a function of deformation and velocity gradient
Dilatancy, Thursday 16h and Friday 13h30
Liquid motion with respect to the bubbles usually arises through gravity (drainage), coalescence or ripening (when a film breaks or when a small bubble vanishes, the corresponding liquid goes to neighbouring films). It has also been observed due to stress and is then called dilatancy. The concept was introduced by Reynolds for granular materials : when a (dry or immersed) granular material is being deformed, it swells (and correspondingly sucks in more air or water). In foams, dilatancy in steady shear deformation was observed by Marse et al., Colloids Surf. A 263 (2005) 121-128. The liquid volume fraction was observed to stabilize at a greater value in regions that displayed a greater shear rate (due to localized shear). This effect is called dynamic dilatancy. Whether foams also exhibit static dilatancy (greated liquid volume fraction where the stress is higher) is not so clear at present. This discussion was more a working session than a discussion. We went over the article Weaire et al. Phil. Mag. 83 (2003) 2747-2760 that deals with static dilatancy (theory and simulation). We went over the mathematics of the article, which takes a thermodynamic approach. We were not entirely convinced by the inversion of two derivatives in Eq.(5). We then discussed whether we could have a clear microscopic understanding of this effect, and we concluded that we did not. (transient) Epilogue. After the workshop (early February), two of us (P. Rognon and C. Gay) went over a more recent article by the same team : Rioual et al. Coll. Surf. A, 263, 117-120 (2005). It is a very similar thermodynamic approach, though quite more detailed. Again, we were confused regarding one particular point (does \Pi differ from \Pi_0 or not?).
Matrix measures of disorder, Thursday 16h
Main discussion : --------------- How can we characterize the disorder of a foam, when all directions are not equivalent? The aim is to quantify a pattern (eg to compare theory, experiment and simulation); and to understand (gain physical insight). Whether in 2D or in 3D, we can measure quantities such as bubble size, number of sides, texture matrix. For each of these quantities, we can characterise the disorder in two ways: - spatial correlations ; for instance, for the bubble area, g(r) = avg(A(0)A(r)) / avg(A^2). It describes whether the bubbles with different areas are well mixed. This is useful if the pattern is heterogeneous at large scale. - spatial fluctuations : for instance, the texture's variance is avg(M(r)^2) - avg(M(r))^2. It describes whether the pattern is heterogeneous at small scale. Open questions : -------------- - are there practical applications? - can it be used to characterise force chains in granular materials? - in foams and emulsions, are there equivalent of force chains? - on what typical sizes should we perform the averages? For instance when there is localisation? - these quantities are for large disorder. What is the link with quantities used to measure weak disorder, eg defects in crystals: Fourier transform, angular and translational correlation functions? - Can we determine, just by looking at a pattern, whether (and where) localisation has occurred?
Effect of disorder on foam properties, Thursday 17h
Let d* represent a measure of disorder.
As a mere starting point, three questions:
1. From the observation of disorder, can we predict where flow will occur?
2. Do properties vary with disorder: yield stress, critical strain rate, effective
viscosity?
3. From a snapshot, can we determine if/where the foam is flowing? is there an order
parameter for flow?
In grains, the answer to point 3. is yes.
Simon: our group is trying to find \sigma_y(d*) and \sigma_y(\Phi).
Question: is a 5-sided bubble wetter?
Suggestion for \sigma_y (Francois G.):
\sigma_Y = G(d*) U_Y(d*)
G(d*) Niels Kruyt implemented six different measures of disorder,
and the variations of G with d* depend on the choice
in the measure of d*
It depends if you vary the disorder while keeping some
average of A = const or some average of sqrt(A) = const or ...
U_Y(d*) is strongly (mainly?) dependent on \Phi, not d*
For simple shear, a sigma-vs-gamma plot
displays an abrupt slope change
(transition from elastic to plastic)
when the disorder is weak,
and it smoothens when disorder increases.
Attempts at answering point 3.
T1s depend on transformation and shear rate.
There are two kinds of flow localization:
1. Usual shear banding (shear rate changes
depending on position across the gap,
while stress is uniform up to Couette curvature).
2. Stress shear banding (shear rate is uniform
up to Couette curvature, but stress changes
depending on position along the vorticity direction).
This second kind of shear banding was described
by Peter Olmsted et al especially
for shear-thickening materials.
Gijs. Experiments on monomodal and on bimodal foams. (2D?)
Monomodal => gliding planes of bubbles near both walls,
mainly plug-flow elsewhere.
Bimodal (disordered) => Same as monomodal at large
shear rates, but uniform shear at low shear rates,
with observed vortices and disordered flow.
(Caution: formula below may be wrong)
Monomodal
V^{2/3} = \partial_y (\partial_y V)^\beta \dot{\gamma}^{2/3}
Bimodal
\sigma = \sigma_y + \eta \dot{\gamma}^{0.36}
(Caution: formula above may be wrong)
Disordered case: global exponent differs from local one:
if the force between two bubbles (local scale)
is taken as proportional to <\Delta V>^{2/3}
the resulting measured stress obeys
\sigma = \sigma_y + \eta \dot{\gamma}^{0.36}
The shear-thinning behaviour drastically changes with disorder.
In a very curved Couette cell,
even a monodisperse foam will display a "disordered behaviour".
Position and width of shear band
as a function of disorder, as measured by \mu_2(n).
Position of shear band:
at (either) wall for small \mu_2
anywhere above some value of \mu_2(n)
Width of shear band is roughly proportional to \sqrt(\mu_2)
for all values of \mu_2, even when shear band is at wall.
Liquid fraction and disorder ?
fewer sides => higher pressure.
Conclusion that it is difficult to sort out
the effect of disorder on liquid fraction
from the simple implication
"smaller bubble => more Plateau border length
per unit volume => wetter foam."
Real 3D structure of quasi-2D foams, Friday 10h
There are three types of quasi-two-dimensional which exhibit different results in
experiment due to major difference in the distribution of liquid within the foam. The
three types of foam are governed by the experimental boundaries or constrictions
placed above or below them in a bubble monolayer. They are the bubble raft (Liquid Air
- LA) or foams between glass plates or liquid or both (Liquid-glass - LG, glass-glass
- GG). The bubble raft experiment is the most difficult for looking at the
distribution of liquid in the foam and therefore for direct comparison with other
foams. It is not clear how a liquid fraction can be accurately measured in the
liquid-air experiment. A key question is how can we get consistent definitions of a 2D
foam in experiment or simulation. Listed below is a list of control parameters and
measurable quantities that acquire careful interpretation for comparison and
consistency of results.
Type of Expt Parameters Measurable Quantities
LA V_b, \rho_b or \Pi_d, L_c = \sqrt{gamma/rho g} A_w (z=z0), A_v, Liquid distribution
GG V_b, d,\Phi_c or \Pi_d, L_c A_w(z=d,z=d/2), A_v
LG V_b, d, L_c A_w(z=z0), A_v
(Where A_w denotes the wetted area of the foam and A_v the area of the vertical films.)
Existing data from simulations (S. Cox):-
- A_v as a function of liquid fraction
- foam liquid fraction as a function of the mean curvature of the films and
wetted area of the foam
It was also discussed whether in the case of long thin bubbles it would be of greater
importance to use the horizontal length of the bubble rather than the vertical length
of the films. The goal is to be able to make good and reliable comparisons of the
different experiments and to improve the simulations (e.g. the Surface Evolver offers
the option of having Plateau borders).
Debate on Constitutive Equations, Friday 11h30
* Definition:
Constitutive equation relates stresses to strains (and strain rate).
* Existence:
On a representative volume element that is larger than the bubble size.
Problems:
- range of single T1
- avalanche of T1
- localisation along zones
* Uniqueness:
A Thermal models
Assume thermally activated probability of plastic transitions.
What is temperature: analogy with disorder ?
- Shear transformation zones by Langer et al. 1998
Two states, switching (T1?) creates plasticity. T1 and reverse T1 can occur?
- Soft glassy rheology by Sollich et al. 1997
Continuous range of deformation before plastic events.
B Phenomenological models
At time scales short in front of aging. They aim at describing:
- Elasticity (transient effect, mechanical model is a spring)
- Plasticity (large amplitude effect, mechanical model is a solid friction element)
- Viscosity (fast deformation effect, mechanical model is a dashpot)
Review of models including these three effects
People, Type, Variables, Space dependence, Comparison with experiments
Janiaud 2006, Unidirectional, Scalar, 1D, Steady Couette with friction
Marmottant 2007, global viscosity and smooth plasticity, Scalar, 0D, Rheometry G? and G?
Marmottant 2008, Tensorial, 2D, Stokes
Saramito 2007, two viscosities, Tensorial, 3D, Steady couette 1D
Benito 2008, plastic viscosity, Tensorial, 3D
Open problems
- How to model viscosity ? One or two viscosities ?
- Large deformations: definition of strain?
- Convective derivative: choice is link to choice of deformation, which on to
choose?
Feedback on the workshop, Friday 14h
If I were organising workshop like this in the future, I would do the following: The same : ------------ - limit the number of people - round table: they are OK to ask questions - room changes: to mark a clear break between discussions - limit to 1h or sometimes to 1/2h - short introduction to each discussion, for beginners - tough chairperson, focused discussions - review of controversial questions - 5' presentations followed by 5' discussions is a good format [see below] - common room to meet, discuss, read e-mail, drink coffee - list of prospective questions - screen participants to keep only specialists of the subject - equilibrate different points of view, especially experiment-simulation-theory - no beamer, no formal speech - formal announcement of informal discussions (even private ones!) - lunch format: self-organised buffet - situated in a lab, to encourage contacts with members of the lab Differently : ------------ - more parallel discussions - encourage beginners to organise more tutorials (early in the week?) - organise the reviews of controversial questions earlier in the week - no lab seminar [NB: it was an explicit request from the lab, in exchange of hosting the meeting] - 5' presentations are too short [see below] - decide a compulsory break afternoon - choose a ski or beach resort - organise better the preprint table, and put it in the common room - allow for photocopies of the preprints - choose odd years, to alternate with even years' Eufoam Comments : ------------- - There were almost no parallel discussions because we were a group with homogeneous interests, and we did not want to miss too many things. With more people the system might be blocked. - 5' presentations should have a clear goal: not to be formal talks, but only to trigger discussions; still, they must be prepared, to convey a clear message in a short time, even to beginners. - it was often hard for beginners / organisers expected they would request more tutorials - compared to a usual congress, the communication was more efficient, the time passed more quickly, there was less stress, it was less tiring, the atmosphere was better, more collaborations made progresses or were initiated.
Most of the discussion was on experimental results. A distinction was made between an overshoot due to structural changes in the material and one that was purely in the elongation angle. Measures of the overshoot focused on the strain tensor and an overshoot in angle. Some evidence for it in simulations and in theory. Theory indicates the importance of the normal stress difference. A question was raised concerning the connection between overshoot and the negative wake in Stoke's flow. Issues of dependence on the usual parameters: liquid fraction, bubble size and disorder.
Jamming transition, Friday 16h
Discussion: Is there a "jamming diagram" for foams? Traditional jamming diagram - load (e.g. stress) vs density (\Phi_l) vs temp. Difference between first and second order phase transitions. Weitz experiment probed diagram, but not others? Could foams? In 2D or 3D? yield stress depends on phi, so jamming well-defined on density axis, but not on local axis. How to interpret temperature, e.g. as disorder? Does \Phi_l - load plane help to explain strain localisation? Do shear modulus and yield stress vanish at the same \Phi_l or disorder? Using disorder as 3rd axis may be easier to control than \Phi_l. How about yield stress (or strain) vs disorder vs \Phi_l as axes? Need strain rate too? How do we define solid/non-solid (e.g. on disorder vs \Phi axes) or flowing/non-flowing (e.g. on yield stress (or strain) axis?