



This challenge is aimed at A-Level students - the first part incorporates decision-based mathematics, whilst the second involves differential equations and integration.
Whilst staying in an Aberystwyth holiday home, Santa decides to make some present deliveries to grottos located in a number of towns around Mid Wales.
As Santa needs to have some rest during his pre-Christmas Eve break, he needs to find the route that will minimize the distance he must travel.
The table below gives the distances between each pair of towns, some of which are shown in this diagram:
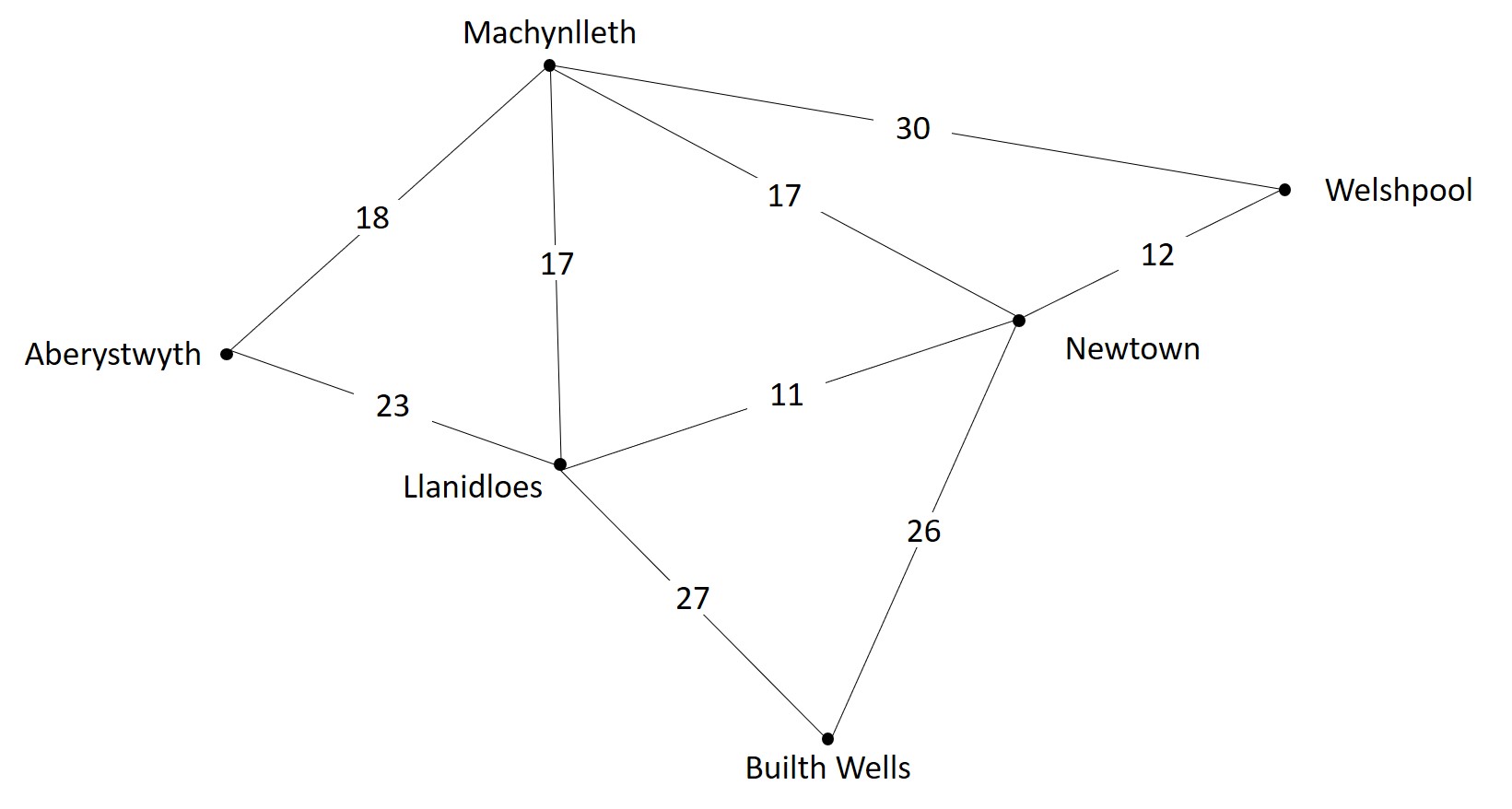
All distances are in miles.
They represent the direct route 'as the sleigh flies', and are the same in both directions.
| Aberystwyth | Builth Wells | Llanidloes | Machynlleth | Newtown | Welshpool | |
|---|---|---|---|---|---|---|
| Aberystwyth | - | 34 | 23 | 18 | 29 | 43 |
| Builth Wells | 34 | - | 27 | 36 | 26 | 37 |
| Llanidloes | 23 | 27 | - | 17 | 11 | 22 |
| Machynlleth | 18 | 36 | 17 | - | 17 | 30 |
| Newtown | 29 | 26 | 11 | 17 | - | 12 |
| Welshpool | 43 | 37 | 22 | 30 | 12 | - |
Challenge 1: Find the route that starts and ends in Aberystwyth and minimizes the distance that Santa must travel to deliver presents to all towns.
Santa's sleigh has a finely tuned electric engine. The drain on the battery depends on the weight of the weight of the sleigh and the current charge.
If the current weight of the sleigh is W (in kg) and the current charge is C, Santa's elves have found that charge is lost at a rate of;
\[{dC \over dt} = -{e^{-C} \over W}\]
Where t is the time since leaving Aberystwyth.
Santa's sleigh moves at a constant speed of 15 mph, and he drops 10 kg of presents at each town.
Challenge 2: Use the route that you found in challenge 1 to determine the amount of charge that the battery must hold (to the nearest unit of charge) when Santa sets out from Aberystwyth, if he delivers presents to the Aberystwyth grotto only on his return.