

Fel arbrawf, gofynnodd Ffred i'r cefnogwyr rygbi ar ddiwedd dwy gêm wahanol am wirfoddolwyr i roi cynnig ar gic adlam. Roedd am weld a oedd bod ar gae'r tîm cartref o fantais. Dangosir y canlyniadau isod
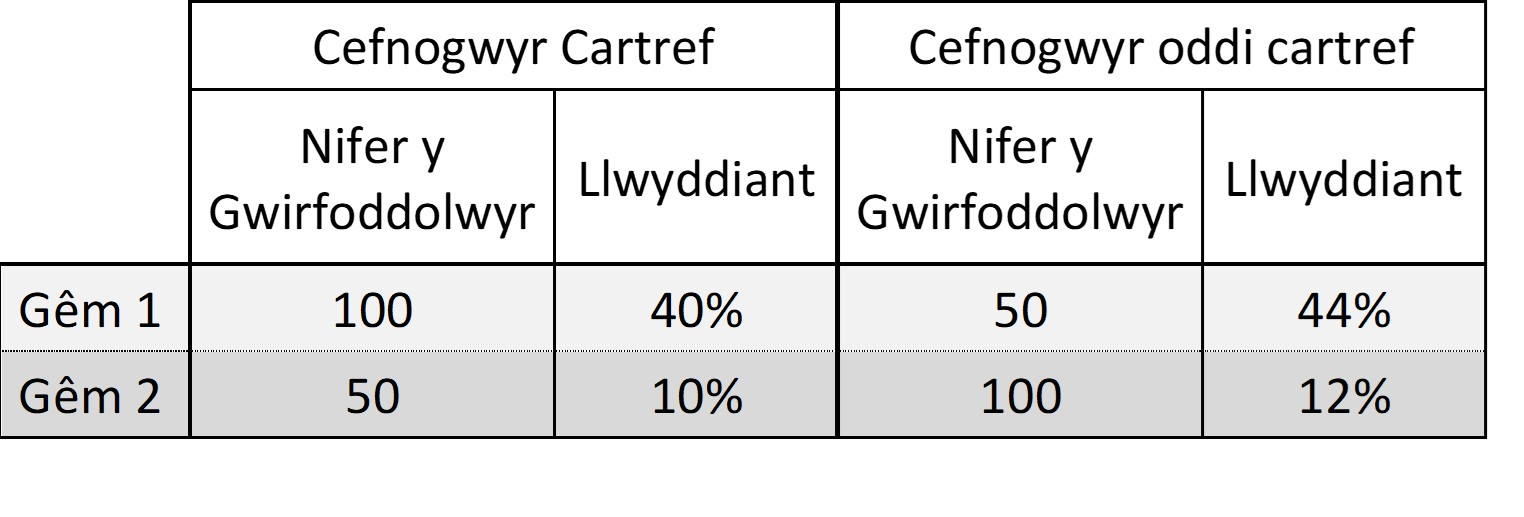
Roedd Ffred yn hapus i gael ei brofi'n gywir, roedd y cefnogwyr ar gae'r tîm cartref yn well na'r cefnogwyr oddi cartref. Sut gall ef brofi hyn?
Bydd yn rhaid i chi weithio allan faint o gefnogwyr oedd yn llwyddiannus ar gyfer y cefnogwyr cartref a'r cefnogwyr oddi cartref.
Mae'n debyg fod y Albert Einstein wedi creu'r pos hwn pan oedd yn blentyn. Gellir goresgyn yr her yma trwy ddefnyddio rhesymeg yn unig.
Mae pum tŷ drws nesaf i'w gilydd, sydd wedi'u paentio'n bum gwahanol liw. Mae person o genedl wahanol yn byw ym mhob tŷ. Mae pum perchennog y tai yn yfed gwahanol fath o ddiod, yn chwarae math penodol o chwaraeon, ac yn cadw anifail anwes penodol. Nid oes gan yr un perchennog yr un anifail anwes, nac yn chwarae'r un math o chwaraeon, nac yn yfed yr un diod.
Pwy biau'r pysgodyn?
Bydd yn rhaid i chi ddefnyddio'r ffeithiau isod i ganfod yr ateb.
Bydd yn rhaid i chi ddefnyddio'r Grid Rhesymu (yn Saesneg). Os nad ydych yn gwybod sut i ddefnyddio grid rhesymu, gallwch wylio tiwtorial ar y wefan posau rhesymu hon.
| Tŷ 1 | Tŷ 2 | Tŷ 3 | Tŷ 4 | Tŷ 5 | |
|---|---|---|---|---|---|
| Cenedligrwydd | Norwyaidd | Danaidd | Prydeinig | Almaenaidd | Swedaidd |
| Lliw | melyn | glas | coch | gwyrdd | gwyn |
| Diod | dŵr | te | llaeth | coffi | cwrw |
| Chwaraeon | pêl fas | pêl foli | pêl droed | hoci | tenis |
| Anifail Anwes | cath | ceffyl | aderyn | pysgodyn | ci |
1, 4, 7, 10, 13 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 40?
1, 3, 9, 27, 81 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 6,561?
1, 3, 6, 10, 15 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 45?
1, 8, 27, 64, 125 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 729?
0, 1, 1, 2, 3, 5, 8 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 55?
4, 9, 25, 49 ...
Beth yw'r ddau rif nesaf yn y dilyniant hwn?
Pa rif sy'n dod ar ôl 961?
Dilyniant 1: Beth yw'r gwahaniaeth cyffredin rhwng pob rhif?
Dilyniant 2: Beth sy'n rhaid i chi ei wneud i'r rhif blaenorol i gael y rhif nesaf?
Dilyniant 3: Meddyliwch am drionglau...
Dilyniant 4: Meddyliwch am giwbiau...
Dilyniant 5: Mae'r dilyniant hwn yn cynnwys adio 2 rif at ei gilydd
Dilyniant 6: Mae'n cynnwys sgwariau rhifau penodol
Mae tri o bobl yn rhannu tŷ ac maent yn archebu pitsa. Pan gyrhaeddodd, gwnaeth y dyn dosbarthu pitsas godi £25 arnyn nhw amdano. Rhoddodd pob un o'r tri £10 iddo. Rhoddodd y dyn dosbarthu newid iddynt, sef pum darn £1. Gan nad oedden nhw'n gallu rhannu hynny'n gyfartal, fe gymerodd pawb un darn £1, gan roi'r £2 arall i'r dyn dosbarthu. Wedyn fe wnaethan nhw sylweddoli bod pob un ohonynt wedi talu £9 i gyd am y pitsa, sy'n golygu bod y cyfanswm wedi dod i £27 ac wedyn eu bod wedi rhoi tip, £2, i'r dyn dosbarthu, sy'n dod i £29 i gyd. I ble aeth y £1 arall?
Sawl gwaith maen nhw'n cynnwys y cildwrn wrth gyfrifo?
Daw'r broblem fathemateg hon o Arholiad Uwch yr Alban gan Awdurdod Cymwysterau'r Alban (2015, Papur 2, Cwestiwn 8).
Mae crocodeil yn hela ysglyfaeth sydd 20 metr i fyny'r afon ar lan arall afon.
Mae crocodeilod yn teithio ar wahanol gyflymdra ar dir ac yn y dŵr.
Gellir lleihau'r amser mae'n ei gymryd i'r crocodeil gyrraedd ei ysglyfaeth os yw'n nofio at fan penodol, P, x metrau i fyny'r afon ar ochr arall yr afon fel sy'n cael ei ddangos yn y diagram.
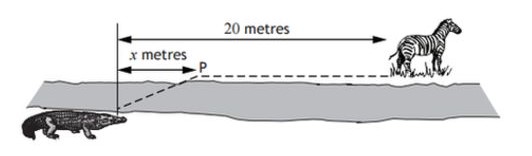
Mae'r amser mae'n ei gymryd, T, yn cael ei fesur mewn degfed ran o eiliad, ac yn cael ei roi trwy
\[T(x) = 5\sqrt{36 + x^2} + 4(20 - x)\]
1. Gyfrifo'r amser a gymerir os nad yw'r crocodeil yn teithio ar y tir.
2. Cyfrifo'r amser a gymerir os yw'r crocodeil yn nofio'r pellter byrraf posibl.
3. Rhwng y ddau eithaf hyn, ceir un gwerth o x sy'n lleihau'r amser a gymerir. Canfyddwch werth x gan felly gyfrifo'r amser lleiaf posibl.
Mae'r hafaliad yn rhoi lled yr afon i chi, chwiliwch am hafaliad Pythagoras.