Maths Challenge 5

Cymraeg

Maths Challenge 5


1: Riddle Basic Operations

I am a two digit number. I am equal to the sum of my digits multiplied by six. What number am I?

Write out the 6 times table until you find the answer that meets the criteria

54 (5 + 4 = 9, 9 x 6 =54)

Percentages

Prices went up by 2% in 2003, 3% in 2004 and 2.5% in 2005.

If an item cost £32 at the start of 2003 what would it cost at the end of 2005?

From "Foundation GCSE Mathematics For WJEC: Homework Book"

Remember: The total from which you are calculating the percentage will change after each year.

Start with £32

In 2003 the price goes up to:
32 + (32 ÷ 100 x 2) = £32.64

In 2004 the price goes up to:
32.64 + (32.64 ÷ 100 x 3) =£33.62 (nearest penny)

In 2005 the price goes up to:
33.62 + (33.62 ÷ 100 x 2.5) = £34.46 (nearest penny)

Fun for all Ages

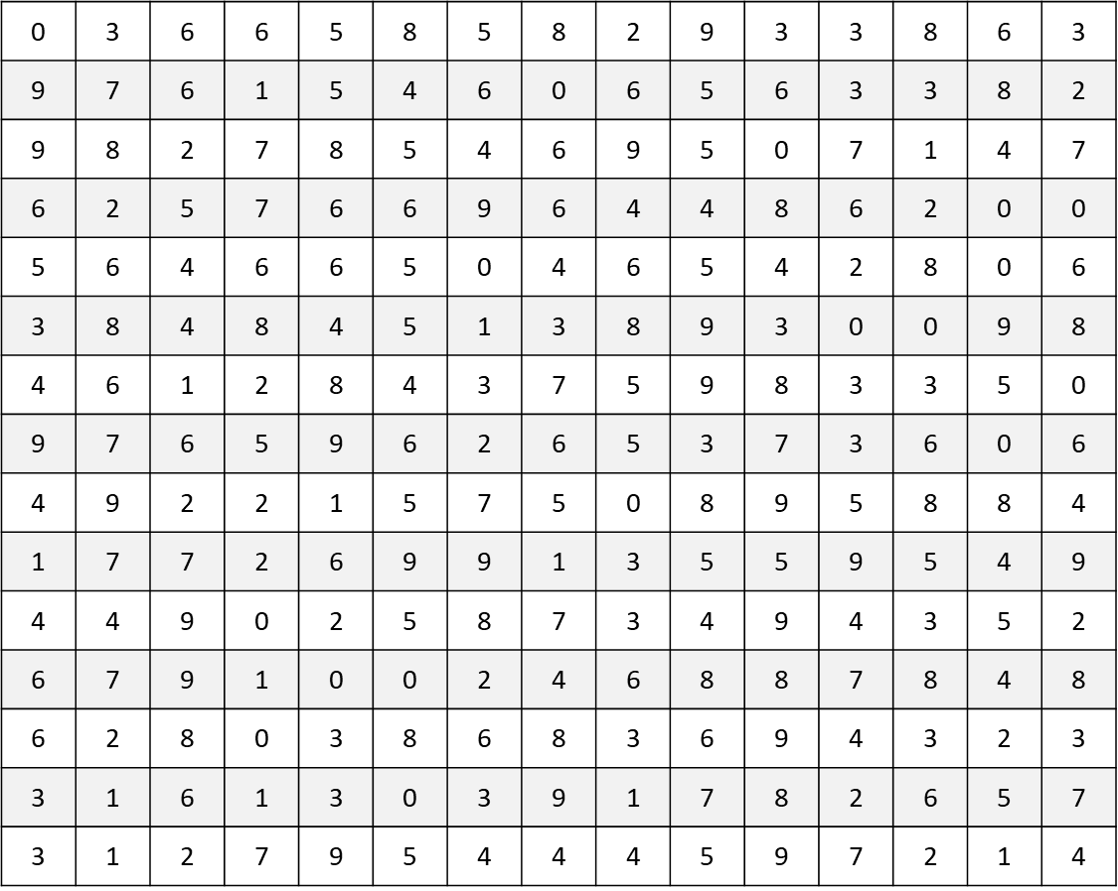
A number search grid
Excel version of number search for screen readers

Find the below numbers in the grid.
The numbers can be in any direction: backwards, forwards, up, down, or diagonally.

128036 438795 638358
132798 456405 658582
170596 466855 689972
247495 473829 782657
257669 488671 826867
274797 489151 855033
376203 524548 865664
389980 606563 868369
400950 608607 954445
414663 626528 989895

Pdf Version Available

From www.puzzles-to-print.com

4: Time KeepingProbability

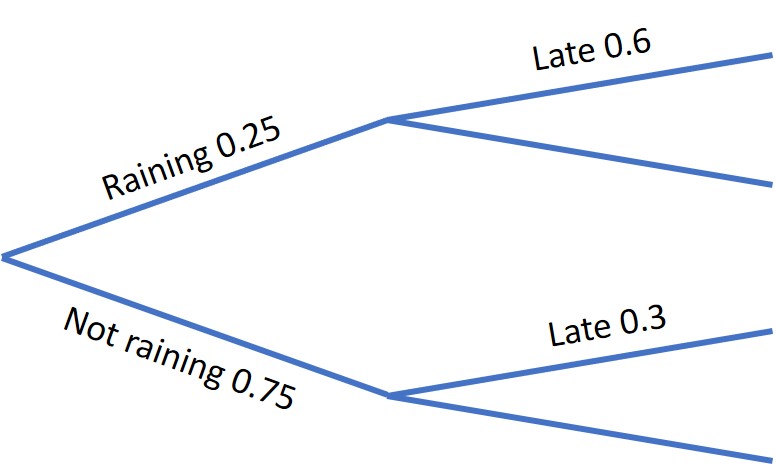
Dafydd is late 60% of the time when it is raining and 30% of the time when it is dry. it rains on 25% of days.

Find the probability that:

  1. It is raining and he is late
  2. He is late

Adapted from "Higher GCSE Maths" by Michael White

Consider using a probability tree to help with this. More information on probability tree diagrams can be found at the Maths is Fun website.

The resultant probability tree:

probability tree
  1. Raining and late
    probability = 0.25 x 0.6 = 0.15 or 15%

  2. Late
    probability = (0.25 x 0.6) + (0.75 x 0.3) = 0.375 or 37.5%

5: Battle ScarsCombinatorics

A group of fifty soldiers suffered the following injuries in battle:

  • 36 lost an eye,
  • 35 lost an ear,
  • 40 lost a leg
  • 42 lost an arm

What is the minimum number of soldiers to suffer all four injuries?

Adapted from: "Einstein's Riddle" by Jeremy Stangroom

Consider the total number of injuries compared to the total number of soldiers.

Total number of injuries = 36 + 35 + 40 + 42 = 153
Total number of soldiers = 50
150 ÷ 50 = 3 with a remainder of 3.
Therefore, a minimum of three soldiers had all four injuries.