

In this exercise we will create a racing dice game and then look at the maths behind what is happening. It's like a maths experiment you can do at home or school.

For this game you will need 2 six-sided dice (either borrowed from a boardgame or printed using this dice template), some paper and a pencil
Imagine you have a straight line race between twelve dragons (each numbered between 1 and 12). The track is 100m long and the first one across the finish line wins. The catch is that each numbered dragon can only move 10 metres when their number is rolled on the dice. For example, if you roll a three and a four then dragon number 7 gets to move 10 metres whilst all the other dragons stay still.
Which dragon do you think would win? Let's give it a go. To keep track of the dragons' movement you will need a table of results. You can have a go at designing one yourself or you could print/copy this blank table of results pdf (for screen-readers, here is the blank table of results in Excel format) to use (feel free to change the dragon names if you wish). Each time a dragon moves you tick the next box for it, so if the dragon has a tick in the 10 metre box and it's number is rolled again then tick the 20 metres box, keep playing until a dragon has all the boxes ticked - that one is the winner.
Was the winner the dragon you thought would win? To make this a better experiment we need to repeat the test. Play the game five more times to see what happens. Don't forget to record those results.
If you are feeling really creative, you could always print off this dragon template or draw your own to create dragon cut-outs that you can design a track for to play with family or friends. Don't forget to put numbers on them, and perhaps names too.
So why do certain dragons win more often than others? To understand what is happening we can draw another type of table - called a matrix, to show all the different possible dice roll totals.
But how do we fill this in? To complete this matrix we fill in each empty box with the total of the column value plus the row value. I have filled in a version for you with the sums needed for each box:
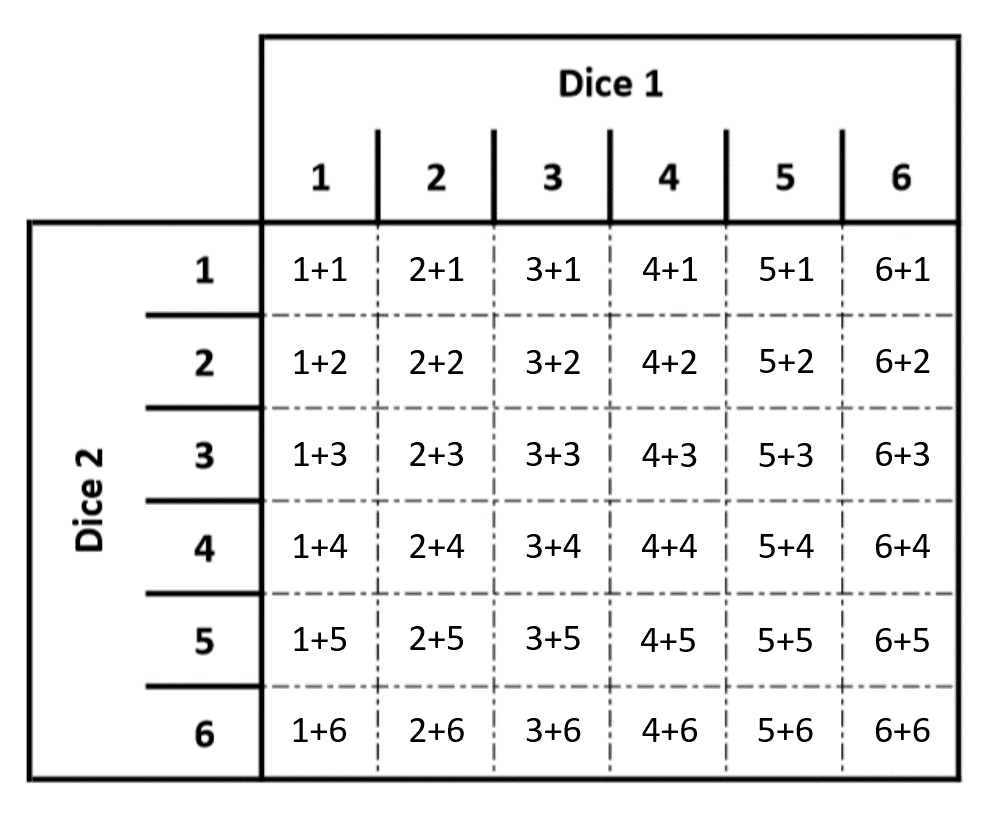
If you are still unsure how to fill in this matrix then here is a copy of the completed matrix in pdf format (for screen-readers, here is the completed matrix in Excel format)
Looking at this matrix we can see all the possible results of rolling 2 six-sided dice. Which number appears the most? Is this the same number that won the most number of your races? Why did dragon number 1 never move?
What would happen if you used 3 four-sided dice instead? To investigate this you will first need a four-sided dice template, unless you happen to own a set of them. Can you show us the maths of what's happening? You will not be able to use a single matrix to show the possible results, so how could you? Just to let you know, there are 64 different combinations of numbers when using 3 four-sided dice.
Why would we not see the same effect if we used a 12-sided dice instead?