

Probability of a draw: 6 out of 36: 6⁄36 = 1⁄6: 1⁄6 × 100 = 16.67%

Probability of Player 1 winning: 21 out of 36: 21⁄36 = 7⁄12: 7⁄12 × 100 = 58.33%
Probability of Player 2 winning: 15 out of 36: 15⁄36 = 5⁄12: 5⁄12 × 100 = 41.67%

Probability of Player 1 winning: 15 out of 36: 15⁄36 = 5⁄12: 5⁄12 × 100 = 41.67%
Probability of Player 2 winning: 21 out of 36: 21⁄36 = 7⁄12: 7⁄12 × 100 = 58.33%
Mean average roll on a standard 6-sided die: (1 + 2 + 3 + 4 + 5 + 6) ÷ 6 = 3.5
Mean average roll with the red die: (1 + 4 + 4 + 4 + 4 + 4) ÷ 6 = 3.5
Mean average roll with the green die: (2 + 2 + 2 + 5 + 5 + 5) ÷ 6 = 3.5
Mean average roll with the blue die: (3 + 3 + 3 + 3 + 3 + 6) ÷ 6 = 3.5
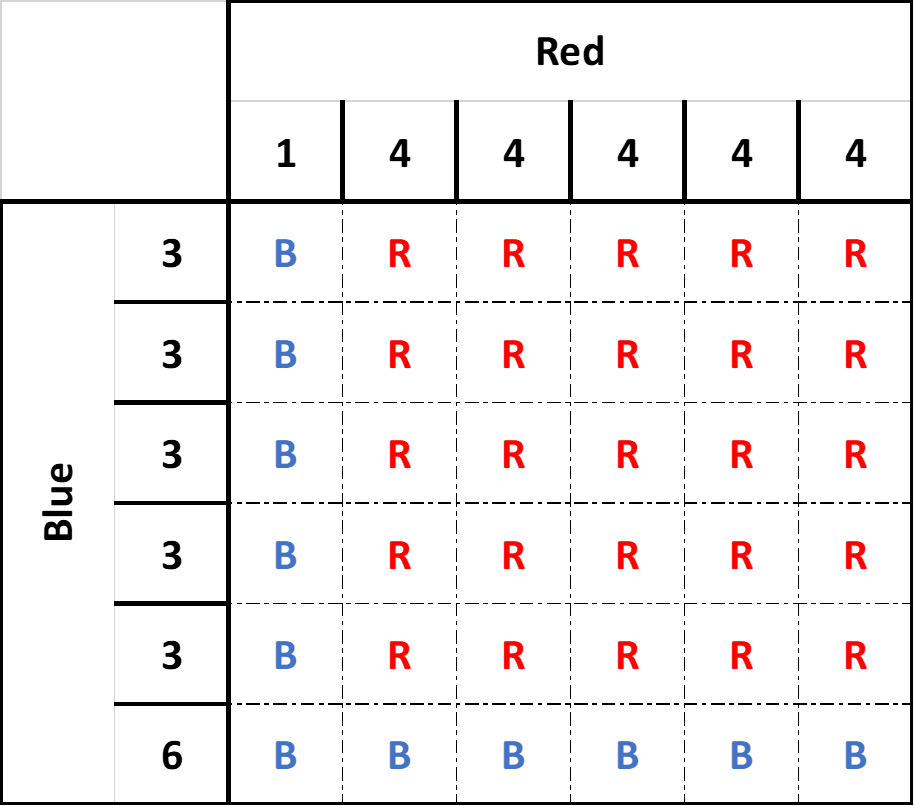
Probability of red winning: 25 out of 36: 25⁄36: 25⁄36 × 100 = 69.44%
Probability of blue winning: 11 out of 36: 11⁄36: 11⁄36 × 100 = 30.56%
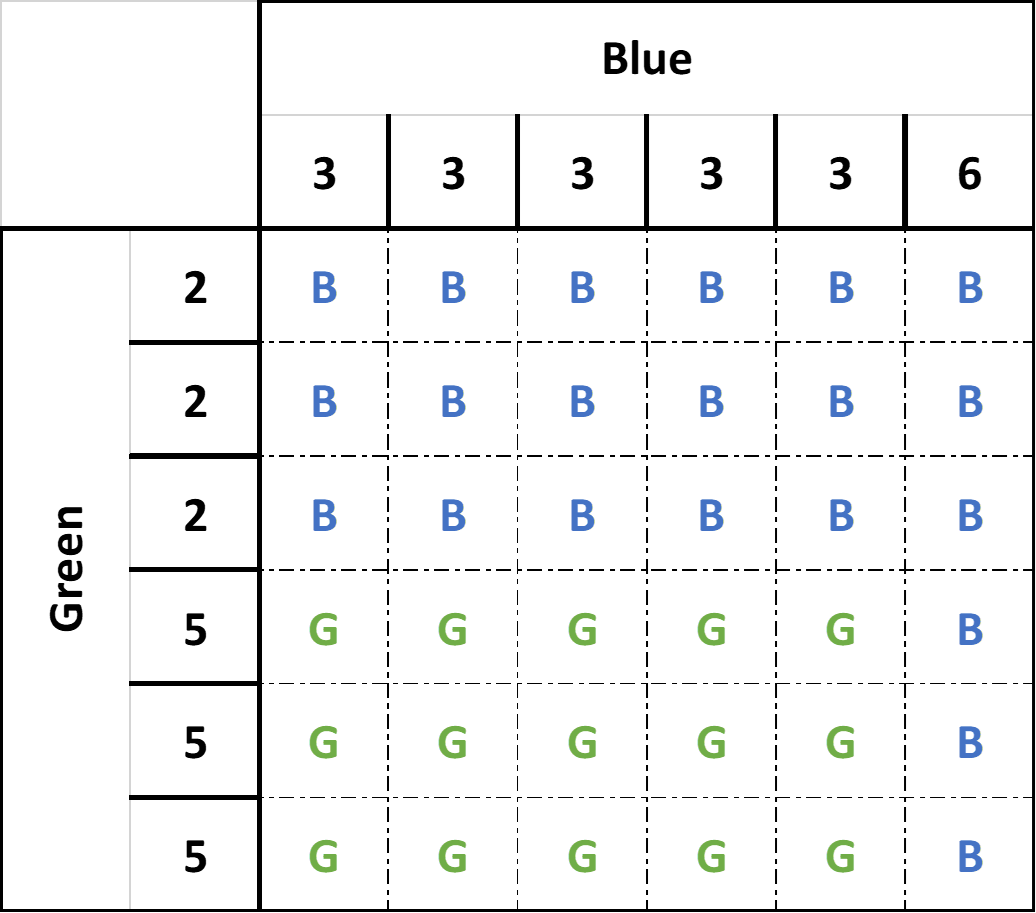
Probability of blue winning: 21 out of 36: 21⁄36 = 7⁄12: 7⁄12 × 100 = 58.33%
Probability of green winning: 15 out of 36: 15⁄36 = 5⁄12: 5⁄12 × 100 = 41.67%
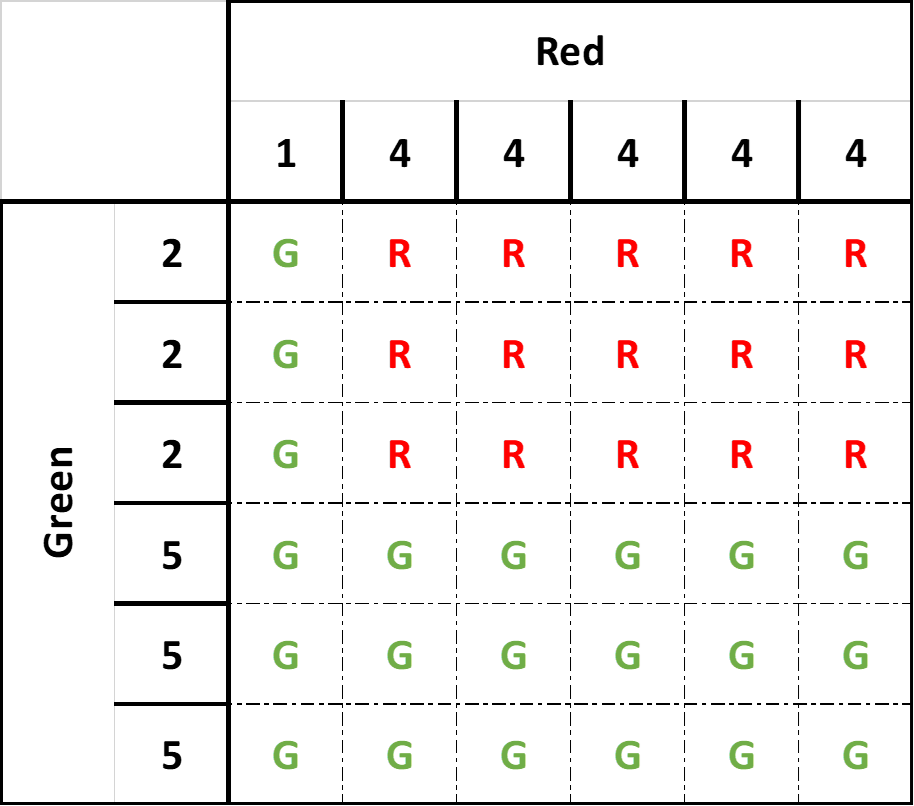
Probability of red winning: 15 out of 36: 15⁄36 = 5⁄12: 5⁄12 × 100 = 41.67%
Probability of green winning: 21 out of 36: 21⁄36 = 7⁄12: 7⁄12 × 100 = 58.33%
So, red beats blue, blue beats green, but green beats red. None of the dice are an outright winner.