Monte Carlo simulation example

This page shows a Monte Carlo simulation which calculates $\pi$. The longer you leave it, the more accurate it will get. It’s just calculating how many points are inside the circle ($C$) compared with how many points are only in the square ($S$). For reasons I’ll go into below, as we generate more and more points $C/S$ will get closer and closer to $\pi/4$.

Here’s how it works. We have a circle inside a square, like the figure below. The square is centred on the origin, each side being $2r$ in length. Our circle is also centered on the origin, with radius $r$.

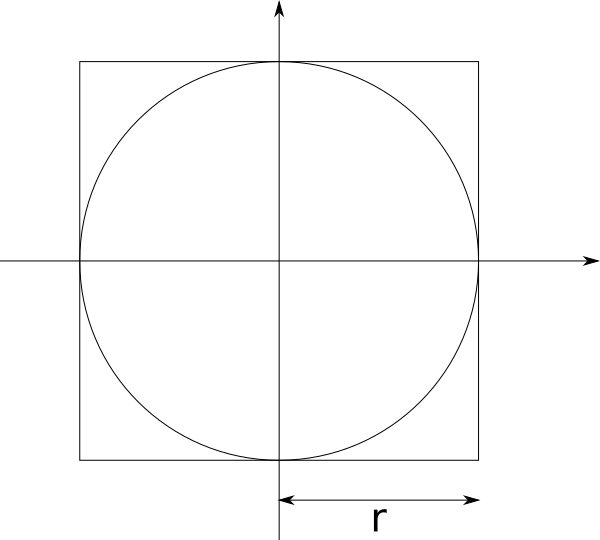
If you remember your basic geometry, you’ll know that a circle of radius $r$ has an area of $\pi r^2$. Our square is $2r$ on each side, so it must have a radius of $4r^2$. So \begin{align} \frac{area\_of\_circle}{area\_of\_square} &= \frac{\pi r^2}{4 r^2} \\
&= \frac{\pi}{4} \end{align} So the area of the circle is $\pi/4$ that of the square.

That means if we just randomly generate points inside the square, there is a $\pi/4$ chance that each point will also be inside the circle. All we need to do is generate hundreds of thousands of points inside a square, and calculate how many of those points are also in the circle. That’s easy, we can just use Pythagoras’ Theorem: for each point generated, it is inside the circle if $$ \sqrt{x^2+y^2}<r $$

So our algorithm is:

• initialise two variables to zero:
  • $S$ is the total number of points in square
  • $C$ is the number of points which are also in the circle
• repeat at least hundreds of thousands of times:
  • generate a random point $(x,y)$ in the square, where $x$ and $y$ are random numbers between $-r$ and $r$
  • increment $S$ (number of points in the square)
  • if $\sqrt{x^2+y^2}<r$, also increment $C$ (number of points in the circle)
  • calculate $t=C/S$ (the ratio of in-circle to not-in-circle). This should gradually approach $\pi/4$ as we add more points
  • Show $4t$, which should get closer and closer to $\pi$.

Source Code

For the curious, here’s the JavaScript source code for the simulation.

// get the canvas and its drawing context 
var canv = document.getElementById("piCanvas");
var c = canv.getContext("2d");

// get just the width - we assume the canvas is square,
// except for a strip of 30 pixels at the top to draw text in.
var w = canv.width;

// clear it
c.clearRect(0, 0, w,w+30);

// and set up the font.
c.font = "30px sans-serif";

// initialise our counts
var C=0; // number of points in circle and square
var S=0; // number of points just in square (=number of points drawn)

// this controls the rate at which we add points - it gets faster as 
// we go along. It's actually the number of points added per frame
var rate =1 ;

// do a single point
function doPoint(){
    // start drawing a path
    c.beginPath();
    // create a point in the range -w to w in x and y
    x = Math.random()*w-w/2;
    y = Math.random()*w-w/2;
    // get the screen coords for that point
    sx = x+w/2;
    sy = y+w/2+30; // remember the strip along the top for text!
    
    // work out the distance from the centre
    d = Math.sqrt(x*x+y*y);
    // is it in the circle?
    if(d < w/2){
        // yes! draw in red and increment C
        c.fillStyle = "red";
        C++;
    } else {
        // no, just draw it in blue
        c.fillStyle = "blue";
    }
    // always increment S, the number of points in total
    S++;
    // draw the point as a tiny circle
    c.arc(sx,sy,2,0,2*Math.PI,false);
    c.fill();
    
    // draw the text along the top
    c.fillStyle = "black";
    c.clearRect(0,0,w,30);
    c.fillText("C="+C,0,28);
    c.fillText("S="+S,200,28);
    r = C/S;
    c.fillText("C/S="+r.toPrecision(4),380,28);
    r = r*4;
    c.fillText("4C/S="+r.toPrecision(5),600,28);
}
    

// does a single frame of animation
function animate() {
    // queue up the next frame
    requestAnimationFrame(animate);
    
    // do "rate" points
    for(let i=0;i<rate;i++){
        doPoint();
    }
    
    // slowly speed up
    rate = rate+0.01;
    // but don't go completely crazy
    if(rate>1000)rate=1000;
    
    
}

// queue up the first frame!
animate();