Image import processing maths

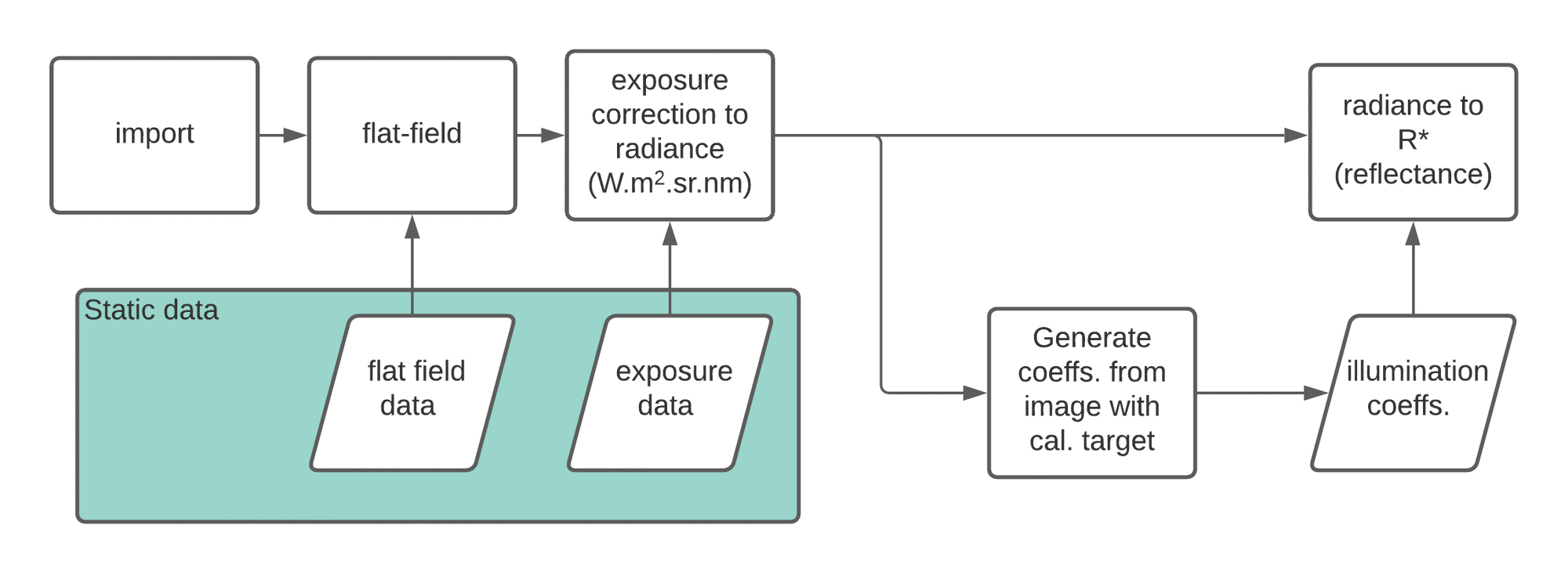
Step 1: Import

Multispectral images are first downloaded from the DAR or imported from disk files (either as ENVI or separate PNG files). Such images may have up to 11 bands.

Step 2: Flat-fielding

Each camera has a set of pixel-to-pixel nonconformities which must be removed. This is done by using a set of flat-field images, one per filter. Processing is done by normalising each flat-field image (so each has a mean of 1) and then dividing each band by the normalised flat-field for that band: $$ Y = \frac{X}{|F|} $$

Step 3: Conversion to radiance

We now produce a calibrated radiance image (W.m².sr.nm). This can be used directly (I believe) or carried forward. We use the equation¹ $$ Y_{\lambda} = \frac{k(t)X}{e_{\lambda}} $$ in which

• $Y_\lambda$ is the output ($\lambda$ is the filter number)
• $k(t)$ is a radiance conversion coefficient dependent on the camera CCD’s temperature $t$
• $X$ is the input image (in digital numbers)
• $e_\lambda$ is the exposure time for filter $\lambda$

Here, $t$ and $e_\lambda$ come directly from image metadata, and $k(t)$ will probably be a lookup table.

Step 4: calculating illumination coefficients

Ideally, these should be captured from the image itself although it’s possible (?) that multiple images could share the same coefficients if they are part of the same set (taken at the same time).

Sources:

1. Allender, Elyse J., et al. “The ExoMars spectral tool (ExoSpec): An image analysis tool for ExoMars 2020 PanCam imagery.” Image and Signal Processing for Remote Sensing XXIV. Vol. 10789. International Society for Optics and Photonics, 2018.
2. Bell III, James F., et al. “In-flight calibration and performance of the Mars Exploration Rover Panoramic Camera (Pancam) instruments.” Journal of Geophysical Research: Planets 111.E2 (2006).