Microbial Growth Website

IBERS: Institute of Biological, Environmental and Rural Sciences

Batch Growth

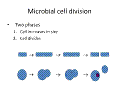
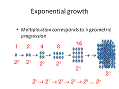
In order to use microbes in industry or research we need to have methods to grow them safely and without contamination. We also need methods to monitor their growth. When we measure the growth of larger organisms such as humans we often repeatedly measure the same individual over a period of time and observe an increase in size. For example the graph below shows the increase in weight of a typical baby boy from 0-3 years (Figure 1).

This approach is impractical with microorganisms for a number of reasons:

1. They are very small so accurate measurement of length, weight etc is very difficult.

2. Repeated measurement of the same individual can perturb (i.e. alter) its behaviour including growth rate.

3. Many microorganisms grow and divide quickly (e.g. E. coli divides every 20 minutes) so measurements would need to be carried out every few minutes.

For these reasons it is usually easier to monitor growth of the population of microorganims rather than of the individual members. If all, or a large proportion, of the cells increase in size the biomass (i.e. weight of viable cells) will increase (Figure 2). Likewise, if the cells divide there will be a change in cell number and this will also cause an increase in biomass from one time point to another. This means that a more practical approach to detecting and quantifying microbial growth is the measurement of biomass concentration.

Bacteria divide exponentially - multiplication corresponds to a geometric progression. One cell divides to become two, these two cells divide to become four, then eight and then sixteen and so on (Figure 3).

This means that if we know the starting concentration of cells and how long it takes a cell to divide we can predict how many cells will be present at a later time point (providing cell division has been occurring exponentially throughout).

The length of time that a cell takes to divide is referred to as the generation time (g). This is the length of time that a newborn cell takes to increase in size, replicate its DNA and synthesise sufficient new cell material to split into two new cells. Again, as individual cells are so small it is easier to work with populations of cells and to measure the time taken for the population to double in number.

If, at the start of an experiment we have an initial number of cells called N₀ (Number of cells at time 0), after n divisions the new cell number (N) in the same volume of the culture is given by the following equation:

  N = N₀ ´ 2ⁿ

So, for example, if we inoculate 1000 bacterial cells into a flask at the start of an experiment, the number of cells after 5 divisions can be calculated as follows:

 N = 1000 x 2⁵ = 32,000

The number of divisions (n) can also be calculated from a knowledge of starting and ending cell concentrations:

n = [log₁₀(N) – log₁₀(N₀)] / log₁₀(2)

For example if we inoculate 1000 bacterial cells into a flask at the start of an experiment and harvest the culture at the end of the experiment and find that we now have 32,000 cells, the number of divisions that has taken place can be calculated as follows:

n = [log₁₀(32,000) – log₁₀(1000)] / log₁₀(2) = 5

Once we know how to calculate n we can use this to calculate other valuable information that we can use to evaluate and optimise growth.

The number of divisions per hour (v) can be calculated using the equation:

v = n / t

where t is the length of time taken for the n divisions to occur.

The generation time g is calculated by

g = 1 / v

So if a culture increases from 10³ to 10⁹ cells per ml in a 10 hour experiment we can calculate the number of divisions as:

n = [log₁₀(10⁹) – log₁₀(10³)] / log₁₀(2)

n = [9 - 3] / 0.3

n = 20

The number of divisions per hour is

v = n / t

v = 20 / 10

v = 2

The generation time is

g = 1 / v

g = 1 / 2

g = 0.5 hours (30 minutes)

A problem for you to try:

In a culture growing in unrestricted exponential growth, at the start of the experiment the culture contains 5000 cells and 7 h later it contains 4x10⁸ cells. Calculate (i) the growth rate v and (ii) the generation time g.

To check your answers and calculations use the workings page for this problem.

All of this assumes exponential growth throughout, such unrestricted growth only occurs provided that nutrients do not become limiting and toxic compounds do not accumulate to an inhibitory level. In unrestricted growth the number of cells in a culture increases at a rate proportional to the number of cells present at a particular time – the population is considered as an autocatalytically multiplying system.

Under such circumstances we can also calculate a specific growth rate (µ) for the organism. The specific growth rate can be an important predictor of the efficiency of conversion of substrate into product. µ is calculated as follows:

µ = [log₁₀(N₂) - log₁₀(N₁)] x 2.303 / (t₂ - t₁)

For example, for a culture that contains 10³ cells at the start of the experiment and 10⁸ cells 6 h later:

µ = [log₁₀(10⁸) - log₁₀(10³)] x 2.303 / (6 - 0)

µ =1.92 h^-1

Now try this problem for yourself:

A flask is inoculated with bacteria at a concentration of 1000 ml^-1 at 9am, at 5pm the bacterial count per ml was found to be 5.5x10⁸. Assuming that there was no lag phase and that there was unrestricted, exponential growth through-out, calculate the specific growth rate (µ) of this culture.

Check your answer and calculations on the workings page for this problem.

 

Figure 1: Graph of baby’s growth. Click for large image.

Figure 2: Microbial cell division has two phases, the cell increases in size and the cell divides. Click for large image.

Figure 3: Exponential growth. Click for large image.