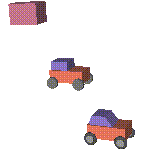
|
|
| Figure 1 | Figure 2 |
|

|
| Figure 3 | Figure 4 |
|
| Figure 5 |
In order to illustrate gnome, a simple (and essentially graphical) example is proposed. The goal is to represent a car for, e.g., a recognition task. Two attributes are represented: geometry and color at three levels of detail which are shown in Figure 1.
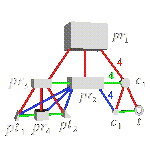
Let us first consider the geometric structure. The car is represented by a rectangular parallelepiped (pr1) at a first level, is split in two rectangular parallelepiped (pr2 for the body and pr3 for the cockpit) and four cylinders (one for each wheel). But the wheels are identical, except for their position. Thus, they will be represented by only one attribute-object (c1). The decomposition arc which links pr1 to c1 is quantified by the value 4 (Figure 2). The geometric attribute-object ``wheel'' is itself split in a rim, represented by a cylinder (c2), and a tire, represented by a torus (t). The cockpit is split in a rectangular parallelepiped (pr4) and two triangular prisms (pt1 and pt2). Figure 2 shows the different geometrical attribute-objects and their decomposition and connection relations.
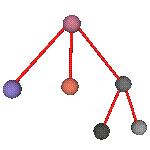
The color's attribute-objects are points in the RGB space. There is a point for each color on the car. The wheels' color at the raw level is a ``mean'' of the tire's and rim's color. This is the same thing for the rectangular parallelepiped representing the car at the rawer level. The corresponding structure is shown in Figure 3. There is no other relation than decomposition.
The quantification of the geometrical attribute-objects is made by associating to the rectangular parallelepiped, cylinders, triangular prisms, and tori an application which specifies their dimensions. For example, for a rectangular parallelepiped, the application is the constant one and simplifies to (w,h,l), a point in R3 representing the width, height, and length of the parallelepiped.
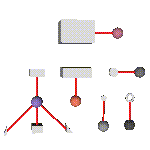
Quantifying the color's attribute-objects is made by locating them in the RGB space (Figure 4).
Only one inter-attributes relation is represented: the correspondence between geometry and color. It gives the color of the different geometrical parts by associating to each geometrical attribute-object a color attribute-object. The graph representing this relation is shown in Figure 5.
More can be found in this report.
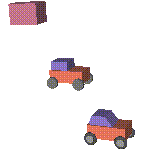
|

|
| Figure 1 | Figure 2 |

|

|
| Figure 3 | Figure 4 |

|
| Figure 5 |